modèle linéaire
La notion de régression est fondamentale dans toutes les sciences appliquées puisqu’elle consiste à analyser une relation entre deux variables quantitatives et à l’exploiter pour estimer la valeur inconnue de l’une à l’aide de la valeur connue de l’autre. Elle est couramment utilisée dans les techniques de gestion et de commercialisation, pour expliquer un chiffre d’affaires en fonction des dépenses publicitaires, effectuer des prévisions de bénéfices, de ventes, etc. Nous formalisons ici la démarche utilisée dans le chapitre 3 pour calculer l’équation de la droite de régression.
1. Modèle de régression simple.
1.1 Variable explicative et variable expliquée.
On étudie en régression deux variables quantitatives, dont l’une, appelée variable expliquée, est considérée comme dépendante de l’autre, appelée variable explicative ou indépendante. On note habituellement la variable expliquée Y, et la variable explicative X.
Lorsque cette dépendance est exacte, la liaison entre les deux variables est « fonctionnelle » : à chaque valeur de X correspond une et une seule valeur possible de Y : cette situation ne présente guère d’intérêt pratique, la relation exacte étant toujours connue.
Lorsque la dépendance n’est pas exacte, la relation que l’on suppose a priori entre les deux variables est approximative : c’est dans ce contexte que la régression apporte des résultats intéressants.
La variable explicative X peut être fixée a priori : on suppose par exemple que le taux d’inflation pour l’an 2003 sera de 1.5% dans les pays de l’Union Européenne, et on en cherche les conséquences sur différents paramètres économiques (taux de chômage, activité, exportations, …) ou sur l’activité économique d’une entreprise : il s’agit en quelque sorte d’un scénario qui n’a aucune raison d’être réalisé puisque les agents économiques vont intervenir en tenant compte des résultats obtenus par la régression.
Elle peut être aussi contrôlée : on mesure la consommation d’une voiture à des vitesses choisies pour établir la relation entre la consommation (variable expliquée) et la vitesse (variable explicative).
La variable explicative peut enfin être observée par tirage au hasard dans une population, comme dans le cas des 50 clients d’EUROMARKET : à une valeur de la variable X (par exemple l’âge, 40 ans), il peut être associé plusieurs valeurs de la variable expliquée Y (par exemple, le revenu, qui n’est pas toujours le même chez les personnes de 40 ans).
1.2 Modèle de régression.
Le modèle de régression est simplement une équation censée représenter cette relation entre les deux variables. Il s’écrit :
|
Y = f(X) + e |
La variable Y est donc supposée approximativement égale à une fonction f de X, le terme e caractérisant la marge d’erreur ou d’imprécision du modèle.
· La variable Y est appelée variable expliquée.
· La variable X est appelée variable explicative.
· La variable e est une variable aléatoire appelée variable résiduelle.
· La variance notée se2 de la variable e est appelée variance résiduelle.
On suppose en outre que le modèle vérifie deux propriétés :
· la variable résiduelle ne dépend pas de X ;
· la moyenne de la variable résiduelle est nulle.
On effectue souvent l’hypothèse supplémentaire que la v.a. e suit la loi normale. Cette hypothèse, qui demande à être vérifiée, permet en effet d’effectuer des tests statistiques et des estimations par intervalle de confiance.
Notre objectif est de préciser la nature de la régression (la fonction f), de mesurer le degré d’imprécision (la variance résiduelle), de détecter les observations qui ne suivent pas le modèle et d’effectuer des prévisions de Y pour différentes valeurs de X (éventuellement par un intervalle de confiance).
Pour effectuer la régression, on dispose de données qui se présentent sous la forme soit d’une suite de n couples [x(i), y(i)], numérotés de i = 1 à i = n (données individuelles), soit d’un tableau de corrélation, ou soit encore de données groupées ou classées. Nous expliquons la méthode dans le cas de données individuelles ; les formules finales sont les mêmes dans tous les cas, à condition de pondérer les observations par les effectifs dans le calcul des paramètres statistiques.
Le modèle de régression est vérifié par chacune de ces observations :
|
Pour tout i de 1 à n |
y(i) = f[x(i)] + e(i) |
Dans l'expression précédente, e(i) est la variable résiduelle e associée aux observations x(i) et y(i).
Nous noterons mx, sx², my,
sy² les moyennes et les variances observées des x(i) et des y(i).
Les propriétés supposées de la variable résiduelle ont comme conséquence que la
variance résiduelle se2 est indépendante des
x(i). Cette propriété est souvent appelée « homoscédasticité »
surtout dans le cas de données économiques.
Exemple :
L’hypermarché EUROMARKET envisage de
commercialiser un crédit par l’intermédiaire de sa carte de paiement et cherche
un moyen de contrôler les revenus que ses clients déclarent en sollicitant ce
crédit. Les données de l’échantillon étant considérées comme fiables, la
méthode choisie consiste à établir une relation entre le revenu et l’âge des
clients, sur lequel il est plus difficile de tricher : le revenu est ici
considéré comme une fonction approximative de l’âge.
Le problème posé est
de vérifier l’existence de la liaison, d’en préciser la nature, le degré
d’imprécision et d’établir une équation permettant d’estimer le revenu d’un
client en fonction de son âge. En appliquant la formule à un client quelconque,
on pourra calculer une valeur approximative de son revenu en fonction de son
âge et valider ou non sa déclaration.
2. Nature de la liaison. graphiques.
2.1 Nature de la liaison
Le premier point de la régression est de déterminer la nature de la liaison entre les deux variables. On privilégie toujours en statistique la liaison la plus simple[1], c’est-à-dire la liaison linéaire entre les variables, de la forme :
f(x) = b x + a
Nous utilisons ici les notations habituelles en statistique : b et a représentent des paramètres théoriques de la régression, et leurs valeurs sont inconnues.
Le choix d’une liaison de nature différente doit être argumenté, par une analyse de chacune des variables ou par une représentation graphique montrant clairement que la liaison ne peut être linéaire. Dans certains cas en effet, on sait a priori que la liaison n’est pas linéaire. Par exemple, un capital de 100€ placé à un intérêt de 10% par an capitalisé n’augmente pas de façon linéaire, mais exponentielle : la première année, il augmente de 10€, la deuxième de 11€ (10% de 110), la troisième de 12.1€ (10% de 121€), ....
Il est clair que dans le cas où le taux d’intérêt n’est pas constant, le même phénomène dû aux intérêts composés se produit et que la liaison entre le temps et le montant du capital actualisé n’est pas en général linéaire.
2.2 Représentation graphique et courbe de régression.
Lorsque l’on ne dispose pas d’information particulière sur les données, la démarche initiale pour étudier la liaison entre deux variables quantitatives est de représenter graphiquement les couples de valeurs observées. On peut alors envisager deux cas.
Si le nombre d’observations est faible, on se limite à
l’analyse de la représentation graphique des couples dont nous avons expliqué
la construction dans le chapitre 3. Sauf contre-indication, on considère la
relation éventuellement mise en évidence comme linéaire,
en prenant soin de rechercher les points aberrants.
Exemple : nous effectuons la régression du revenu des 50 clients par leur âge. Pour un nombre d’observations égal à 50, on peut se limiter à la représentation graphique des couples : nous avons déjà constaté la particularité des clients de rang 25, 31 et 43 sur la figure 2 du chapitre 3. En dehors de ces trois clients, on peut considérer que la liaison est linéaire puisqu’aucune autre relation n’apparaît clairement.
Si le nombre d’observations le permet, on étudie la courbe de régression. Cette courbe représente la fonction de régression f de la même façon que l’histogramme représente la densité théorique d’une v.a.. On procède de la façon suivante pour la construire :
1) On répartit les observations de la variable explicative dans k intervalles, en repérant le rang des unités statistiques de chaque intervalle. Chaque intervalle est caractérisé par son centre cxl ou sa moyenne mxl considérée comme valeur approximative des observations de l’intervalle.
2) On calcule la moyenne des observations de la variable expliquée pour les unités statistiques de chaque intervalle précédent. On obtient k moyennes myl, l = 1, …, k .
3) On représente graphiquement les k couples [mxl, myl] ou [cxl, myl], éventuellement par un disque d’aire proportionnelle à l’effectif nl: on obtient ainsi la « courbe de régression ».
4) On analyse ensuite le graphique comme précédemment : on suppose que la courbe de régression est linéaire sauf contre-indication. La fonction f(x) est de la forme b x + a.
Exemple : Pour construire la courbe de régression du revenu par l’âge, nous avons défini 4 intervalles d’âge de même amplitude :
|
k |
effectif nk |
centre cxk |
âge moyen mxk |
rangs observations x(i) |
revenu moyen myk |
|
|
88 400.86 |
||||||
|
111 350.99 |
||||||
|
141 014.6 |
||||||
|
108 204 |
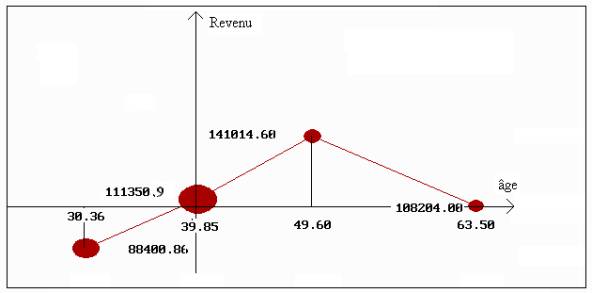
Figure 1.7 : représentation graphique de la courbe de régression du revenu par l’âge.
(origine des axes : valeurs moyennes)
On a pour l’intervalle 4 :
my4 = [y10 + y25 + y43 + y31 ] / 4 = 108 204.
L’interprétation de la courbe de régression aboutit évidemment à la même conclusion que précédemment : l’intervalle 4 rend impossible une liaison linéaire.
Il existe un paramètre statistique classique pour mesurer la proximité de la courbe de régression aux valeurs observées : c’est le rapport de corrélation de Y par X, qu’il ne faut pas confondre avec le coefficient de corrélation linéaire. Il est fondé sur la décomposition de la variance de la variable expliquée lorsque les n observations sont réparties en k groupes.
Définitions : lorsque les n observations y(i) i = 1, …, n sont réparties en k groupes d’effectifs nl :
· on appelle variance totale sT2 la variance des observations (y(i)) i = 1, ..., n :
|
|
|
1 |
n |
|
|
sT2 |
= |
–– |
S |
[ y(i) - my ]2 |
|
|
|
n |
i = 1 |
|
· on appelle variance expliquée (ou inter) sm2 la variance des moyennes myl des groupes pondérées par les effectifs nl des groupes :
|
|
|
1 |
k |
|
|
sm2 |
= |
–– |
S |
nl (myl - my)2 |
|
|
|
n |
l = 1 |
|
· on appelle variance résiduelle (ou intra) sr2 la moyenne des variances syl 2 calculées dans chacun des groupes pondérées par les effectifs nl des groupes.
|
|
|
1 |
k |
|
|
sr2 |
= |
–– |
S |
nl syl 2 |
|
|
|
n |
l = 1 |
|
propriété fondamentale : la variance totale sT2 est égale à la somme de la variance expliquée sm2 et de la variance résiduelle sr2 :
|
sT2 = sm2 + sr2 |
La propriété fondamentale que nous admettons ici est démontrée dans l’exercice 7 du chapitre 2. La notion de variance résiduelle est analogue à celle qui a été introduite dans le modèle de régression, la fonction f étant définie par la courbe de régression.
Définition : on appelle rapport de corrélation de Y par rapport à X le rapport h2 de la variance expliquée à la variance totale :
|
|
|
sm2 |
|
h2 |
= |
–––– |
|
|
|
sT2 |
Propriétés du rapport de
corrélation :
· le rapport de corrélation est compris entre 0 et 1 ;
· une valeur proche de 1 montre que la valeur y de la variable expliquée Y ne varie pas beaucoup à l’intérieur de chaque classe (sr2 » 0, sm2; » 1), et est assez bien déterminée par la classe à laquelle la valeur x appartient ;
· une valeur proche de 0 montre que les moyennes myla sont très proches les unes des autres (sm2 » 0) et que la valeur x de la variable explicative X ne donne guère d’indication sur la valeur y de la variable expliquée Y.
Le rapport de corrélation mesure la liaison entre les variables indépendamment de la nature de cette liaison, contrairement au coefficient de corrélation qui la suppose linéaire.
Pour en apprécier approximativement la taille, on peut en calculer la racine carrée et la comparer à celle d’un coefficient de corrélation. Mais, si l’on suppose que la variable Y suit la loi normale de moyenne m et de variance s2 dans chaque classe, il existe un test.
Théorème : Si le rapport de corrélation théorique est nul, la statistique F :
|
|
|
(n – k) |
h2 |
|
F |
= |
¾-¾ |
-¾¾- |
|
|
|
(k – 1) |
(1 - h2) |
suit la loi de Fisher de degré de liberté k - 1, n - k.
Test de nullité du rapport de corrélation :
· Hypothèse nulle :h2 = 0 (ou Y de même moyenne théorique dans chaque classe).
· Hypothèse alternative :h2 ¹ 0 (ou au moins une moyenne différente des autres).
· Statistique du test :variable F définie précédemment.
· Région critique :] fa, + ¥ [, fa étant obtenu par lecture de la table de la loi de Fisher pour un risque de première espèce a.
Exemple : Le rapport de corrélation du revenu par l’âge est égal à 0.2537. Le calcul donne f = 5.21, pour une région critique ]2.81, + ¥ [avec un risque de 5%. On rejette l’hypothèse de nullité. Mais il faudrait vérifier les hypothèses sur la variable expliquée Y.
On peut aussi considérer que sa racine carrée, de l’ordre de 0.5, est relativement proche de 1 par analogie avec un coefficient de corrélation linéaire de 0.5 pour n = 50.
|
Gr. |
Effectif |
Moyenne mxl |
Moyenne myl |
Variance syl 2 |
|
1 |
14 |
30.357 |
88400.857 |
51 643 044.8367 |
|
2 |
27 |
39.852 |
111350.852 |
589 543 173.5336 |
|
3 |
5 |
49.600 |
141014.600 |
1 120 468 325.8400 |
|
4 |
4 |
63.500 |
108204.000 |
2 621 834 260.5000 |
On en déduit :
|
Variance totale de la variable expliquée sT2 |
877 095 300.2096 |
|
Variance expliquée de la variable
expliquée sm2 |
222 488 353.3638 |
|
Variance résiduelle de la variable
expliquée sr2 |
654 606 946.8458 |
|
Rapport de corrélation de Y par X h2 |
0.2537 |
3. Modèle linéaire.
Nous allons supposer maintenant qu’il est raisonnable de supposer que la liaison entre les deux variables étudiées soit linéaire. Le modèle de régression s’exprime donc de la façon suivante :
Définition : on appelle droite de régression théorique la droite d’équation y = b x + a, et coefficients de régression théoriques les coefficients b et a.
3.1 Critère des moindres carrés
Le problème consiste à calculer les coefficients de régression. Nous ne pouvons évidemment calculer les valeurs exactes, mais seulement des estimations, que nous noterons b pour b et a pour a.
Nous avons représenté sur la figure 2 deux points i et i’ caractérisant les couples [x(i), y(i)] et [x(i’), y(i’)] parmi les n couples. L’objectif est de déterminer les coefficients de la droite y = b x + a la plus proche possible des n points.

Figure 2.7 : critère des moindres carrés dans le modèle linéaire
Plus précisément, il s’agit de reconstruire le mieux possible la variable Y en fonction de la variable X, et donc de déterminer la droite de façon à ce que les termes d’erreur de la forme e(i) = y(i) – [b x(i) + a ] soient les plus petits possible, les plus proches de 0.
Nous avons défini dans le chapitre 2 deux critères pour mesurer la proximité de la valeur 0 à ces erreurs : la somme des valeurs absolues et la somme des carrés de ces termes. Pour des raisons diverses, de calcul en particulier, ce sont les carrés que l’on considère généralement (mais l’autre méthode existe) et l’on cherche donc les coefficients b et a tels que la somme des carrés soit minimale ; d’où l’expression « droite des moindres carrés », fréquemment employée pour désigner la droite de régression.
3.2 Estimation des coefficients de régression.
Théorème : les estimations b et a des coefficients de régression théoriques b et a sont telles que la somme des carrés des erreurs soit la plus petite possible. Elles sont données par les formules ci-dessous :
|
|
|
cov(x,y) |
|
|
sy |
|
|
|
b |
= |
¾-¾¾ |
= |
r(x,y) |
-¾ |
|
|
|
|
|
sx2 |
|
|
sx |
|
|
|
a |
= |
my - b mx |
|
|
|
|
|
Ces formules dépendent des moyennes mx et my, de la covariance cov(x,y), des écarts-types sx et sy, et du coefficient de corrélation r(x,y) que l’on calculera avec les formules adaptées au cas des données individuelles, des données groupées, ou des tableaux de corrélation. Les démonstrations des formules sont données dans les compléments pédagogiques.
Les estimations b et a sont appelées coefficients de régression estimés. Ce sont les valeurs observées des estimateurs empiriques B et A. La droite y = b x + a est la droite de régression estimée (on omet souvent le terme « estimé »).
Remarque : la droite de régression passe par le point moyen :
pour
x = mx, on obtient y = my.
Exemple : nous avons vu dans le chapitre précédent que la liaison entre l’âge et le revenu des clients de l’hypermarché peut être considérée comme linéaire lorsqu’on se limite aux personnes en activité, c’est-à-dire lorsqu’on élimine les clients 25, 31 et 43.
On a effectué ici la régression du revenu par l’âge tout d’abord sur toutes les observations, puis après avoir effectué cette élimination. Les droites de régression ont pour équations :
|
Estimation du Revenu = 946.174 x âge + 69735.75 |
(toutes les observations) |
|
Estimation du Revenu = 2875.963
x âge - 1028.645 |
(après élimination) |
Nous avons représenté l’ensemble des 50 couples, la droite de régression obtenue en effectuant les calculs sur la totalité des observations et la droite de régression obtenue après élimination des clients 25, 31 et 43 (figure 3).

Figure 3.7 : régression linéaire du revenu par l’âge
avec et sans les clients n° 25, 31 et 43
Les deux droites de
régression sont très différentes l’une de l’autre : la première passe par
l’origine des axes (point moyen des 50 observations), et la seconde passe par
le point moyen calculé sur les 47 observations, différent donc du précédent.
Les trois clients 25, 31 et 43 perturbent
nettement les calculs.
4. étude des résidus.
Une régression complète ne se limite pas au calcul des estimations : il est indispensable de valider le modèle estimé, c’est-à-dire de vérifier son adéquation aux données analysées. Pour cela, on utilise les résidus.
4.1 Résidus.
La droite de régression théorique a pour équation :
y = b x + a
Les coefficients de régression théoriques b et a sont évidemment inconnus, et on ne dispose que des estimations b et a de ces coefficients.
À chaque valeur x(i) on peut associer l’estimation b x(i) + a de Y donnée par la droite de régression, et la comparer à la valeur observée y(i) : on obtient ainsi le résidu e(i), qui est l’écart entre la valeur observée y(i) et la valeur b x(i) + a estimée par la régression.
Définition : on appelle résidus les erreurs observées e(i) définies par :
e(i) = y(i) – [ b x(i) + a ]
Les résidus sont des approximations des erreurs inconnues e(i) :
e(i) = y(i) – [ b x(i) + a ].
On montre qu’ils sont centrés (de moyenne nulle) et que leur covariance, donc leur coefficient de corrélation, avec la variable explicative est nulle :
|
|
|
1 |
n |
|
|
|
|
|
me |
= |
––– |
S |
e(i) |
|
= |
0 |
|
|
|
n |
i = 1 |
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
cov (e,x) |
= |
––– |
S |
e(i) |
[x(i) –
mx] |
= |
0 |
|
|
|
n |
i = 1 |
|
|
|
|
Leur variance est égale à la moyenne de leurs carrés puisque leur moyenne est nulle :
|
|
|
1 |
n |
|
|
1 |
n |
|
|
se2 |
= |
–––– |
S |
(e(i) –
me )2 |
= |
–––– |
S |
e(i)2 |
|
|
|
n |
i = 1 |
|
|
n |
i = 1 |
|
La variance étant un ordre de grandeur des carrés des résidus, l’écart type se donne donc un ordre de grandeur des résidus.
La variance se2, que nous noterons simplement s2 conformément à l’usage, s’exprime en fonction du coefficient de corrélation par la formule suivante :
|
s2 = (1 – r2
) sy2 |
Exemple : Calculons quelques résidus dans la régression du revenu par l’âge :
|
x1 = 51 ans, |
y1
= 195 888 F, |
b x1 + a = 145 645.4
F : |
e1 = 50242.6 F |
|
x26 = 45 ans, |
y26
= 107808 F, |
b
x26 + a = 128389.7 F : |
e26 = -20 581.7 F |
Le coefficient de corrélation est égal à 0.6728 et son carré à 0.4527. On en déduit la variance des résidus :
s2 = (1 – 0.4527) = 0.5473 x 874 467 804.91 = 478 596 229.62
L’écart type des résidus (s = 21 876F) est nettement plus petit que celui des revenus (sy = 29 571.4F). L’âge apporte donc une information importante sur la dispersion des revenus observés.
4.2 Propriétés des résidus.
Le modèle théorique n’est satisfaisant que si les résidus possèdent un certain nombre de propriétés :
· Les résidus et la variable explicative doivent être indépendants. Ce second point peut aussi être contrôlé graphiquement : on représente graphiquement les couples [x(i), e(i)] ou, ce qui revient au même, les couples [b x(i) + a, e(i)] pour détecter une liaison éventuelle entre les deux variables [x(i)] et [e(i)]. Rappelons que cette liaison ne peut être linéaire puisque le coefficient de corrélation entre les résidus et la variable explicative est nul : on pourra trouver par exemple un nuage de points en forme de parabole, dont nous donnons un exemple dans le chapitre 3. La vérification de cette hypothèse est indispensable dans le cas d’observations échelonnées dans le temps (cf. chapitre 8).
· On connaît la propriété suivante fondamentale :
s2 = (1 – r2 ) sy2
Pour apprécier la qualité de l’ajustement linéaire, on peut donc utiliser le coefficient de corrélation entre les séries [x(i)] et [y(i)] : un coefficient de corrélation dont le carré est proche de 1 indique des résidus relativement petits par rapport à la variable expliquée. Rappelons que cela ne suffit pas à justifier le modèle linéaire.
On peut contrôler que la variable résiduelle e suit la loi normale en effectuant un test d’ajustement du c2 sur les résidus, bien qu’ici ce test ne soit pas très bien adapté (les procédures correctes sont assez compliquées). La répartition des résidus suivant la règle de classification expliquée dans le chapitre 2 doit donner approximativement les pourcentages correspondant à la loi normale. Cette propriété est surtout utile pour estimer les coefficients de régression et effectuer des prévisions à l’aide d’intervalles de confiance.
Exemple : dans la régression du revenu par l’âge
(après élimination des clients de rang 25, 31 et 43), l’histogramme des résidus
donné ci-dessous en figure 4 montre une certaine asymétrie de leur répartition.
La courbe superposée représente la densité de la loi normale de même moyenne et
de même variance ; la proximité ne semble pas très bonne, mais il y a peu
de résidus dont la valeur absolue soit particulièrement grande.
Histogramme des résidus (régression du revenu par l’âge)
cinq classes de même
amplitude
Pour effectuer le test d’ajustement du c2 nous avons regroupé les deux derniers
intervalles de façon à assurer la convergence de la loi de la statistique X2
vers la loi du c2.
Le degré de liberté est donc égal à n = k
– l – 1 = 2, puisque seule la variance est estimée à partir des données ( k =
4, l = 1).
On trouve :
|
x2
= 3.911 |
ddl: ν = 2 |
P(X2>3.911) =
0.13899 |
On peut donc considérer
que la répartition des résidus est gaussienne (notons que si l’on choisit un
degré de liberté égal à k – 1 au lieu de k – l – 1 comme nous l’avons proposé
dans le chapitre 7, la probabilité critique est égale à 0.27 : la décision
est la même).
La représentation des
couples [e(i), x(i)] (figure 5), ne montre pas de liaison particulière entre
les résidus et la variable explicative (les u.s. ont été renumérotées de 1
à 47) :

Figure 5.7 : représentation graphique des couples (âges, résidus)
(47 couples)
En conclusion, le modèle de régression linéaire donne des résultats relativement satisfaisants.
5. Prévisions.
La question que l’on se pose maintenant est de savoir si le modèle ajusté a un sens sur l’ensemble des clients, et dans quelle mesure il permet d’effectuer des prévisions correctes.
5.1 Estimation et intervalle de confiance de la variance résiduelle.
La variance résiduelle se2 est par définition la variance de la variable résiduelle e. On en obtient une valeur approchée à l’aide de la variance s2 des résidus.
En fait, on utilise plutôt le terme s’2 = n s2 / (n-2). Ce terme possède la propriété d’être sans biais : à chaque échantillon d’observations [x(i), y(i)] i=1, ..., n correspond une valeur s’2, et la propriété « sans biais » signifie que lorsque l’on tire une infinité d’échantillons de taille n, la moyenne des s’2 est égale à la variance résiduelle se2 (cf. chapitre 5).
Définition : l’estimation « sans biais » de la variance résiduelle est égale à
|
|
|
n |
|
|
s’2 |
= |
––––– |
s2 |
|
|
|
n – 2 |
|
s2 étant la variance des résidus et n le nombre d'observations.
Une autre propriété des résidus est que la variable X2 = n S2 / se2 suit la loi de probabilité du c2 de degré de liberté égal à n-2, lorsque la variable résiduelle suit la loi normale. On peut donc en déduire l’intervalle de confiance de la variance résiduelle pour un niveau de confiance fixé comme nous l’avons expliqué dans le chapitre 5, la seule différence étant le degré de liberté et la forme de l’intervalle de confiance.
Exemple : le carré du coefficient de corrélation linéaire dans la régression du revenu par l’âge est égal à r2 = 0.4527. On en déduit la variance des résidus et l’estimation sans biais de la variance résiduelle :
|
s2 = 480 034 257.8 |
et |
s’2 = 501 369 113.7 |
Cherchons l’intervalle de confiance de la forme ]0, c20.05 [, qui donnera la valeur maximale possible de la variance résiduelle pour un niveau de confiance choisi.
|
P(n S2 / s2 > c20.05 ) =0.95 |
d’où |
P(s2 < n S2 / c20.05 ) =0.95 |
On trouve dans la table du c2 pour un degré de liberté égal à 45 et un niveau de confiance de 95% c20.05= 30.612. D’où :
Intervalle de confiance de la
variance : [0, 737 018 493.3]
Intervalle de confiance de l’écart type : [0, 27 148.08]
On notera que cet intervalle ne contient pas l’écart type de la variable expliquée (sy = 29 571.4). On a en fait testé et rejeté l’hypothèse nulle r = 0.
5.2 Test sur les coefficients de régression.
En règle générale on se borne à l’étude du coefficient de régression b dans l’équation
y = b x + a
On peut se poser deux questions :
· La liaison existe-t-elle réellement ?
· Est-il possible d’estimer b à l’aide d’un intervalle de confiance ?
Pour répondre à la première question, il faut procéder à un test statistique sur b : si la valeur b = 0 est vraisemblable compte tenu des données, on ne peut affirmer que la liaison existe. Ce test est en fait plus ou moins équivalent au test sur le coefficient de corrélation r des couples [x(i),y(i)] i = 1, …, n que nous avons présenté dans le chapitre précédent[2].
Exemple : La répartition des résidus étant à peu près normale, nous pouvons effectuer un test sur le coefficient de corrélation. La procédure est celle que nous avons suivie dans le chapitre 6, en testant la liaison entre l’âge et le logarithme des revenus (ici, nous considérons les revenus et non leur logarithme). Les tables donnent comme seuils ra2 et fa pour 45 degrés de liberté :
|
ra2 = 0.08237 |
ra = 0.287 |
fa = 4.05 |
Ce coefficient est égal à r = 0.6728. On en déduit f = 37.22. On rejette donc l’hypothèse r = 0 : la liaison existe indépendamment du hasard.
Définition : on appelle intervalle de confiance du coefficient de régression b au niveau de confiance (100-a)%, l’intervalle :
|
|
|
s’ |
|
s’ |
|
|
[ |
b – ta |
––– |
, b + ta |
––– |
] |
|
|
|
(n sx) |
|
(n sx) |
|
dans lequel ta est choisi dans la table de Student en fonction du niveau de confiance 1 – a et du degré de liberté n = n – 2, s’2 est l’estimateur sans biais de la variance résiduelle et sx l’écart type observé de la variable explicative.
Cet intervalle donne l’ensemble des valeurs acceptables de b. S’il contient la valeur 0, cela signifie que les données ne permettent pas d’affirmer que le coefficient de régression b est différent de 0 ni que la liaison existe.
Exemple : Le coefficient de régression b est égal à 2875.963 ; nous ne
développerons pas les calculs qui aboutissent à l’intervalle de
confiance pour un niveau de confiance de 95% :
Intervalle de confiance de b : [ 1952.02, 3799.89 ]
Cet intervalle de confiance ne contient pas
la valeur 0 : le coefficient de régression b
ne peut être nul compte tenu des observations effectuées.
En général, on prendra garde à ne pas
interpréter trop vite l’estimation b du coefficient de régression b.
Sa valeur numérique n’est pas suffisante pour pouvoir affirmer que b
est non nul : pour pouvoir effectuer cette comparaison, il est
indispensable de calculer l’intervalle de confiance de b comme ci-dessus , ou
d’effectuer le test de Student pour tenir compte de son écart-type (ce test est
effectué dans la plupart des logiciels).
5.3 Prévision ponctuelle et par intervalle de confiance.
Un des objectifs de la régression est de permettre d’effectuer des estimations de la variable expliquée en fonction de la variable explicative. On utilise souvent le terme prévision au lieu d’estimation même si les données ne sont pas temporelles.
Le calcul est simple, mais il faut savoir précisément ce que l’on estime. En effet, le modèle linéaire est le suivant :
y = b x + a + e
On remplace bien sûr b et a par
leurs estimations b et a pour effectuer le calcul ; mais la présence de la
variable résiduelle, dont la moyenne est nulle, montre que l’estimation que
l’on effectue est celle de la moyenne des y pour la valeur x choisie.
Exemple : la régression du revenu par l’âge a donné
l’équation ci-dessous (47 observations) :
Estimation du revenu
= 2875.963 x âge - 1028.645
Lorsque l’âge est égal à 40 ans,
l’estimation du revenu est de 114 009.86 F. La signification précise est la
suivante : la moyenne des revenus des clients de 40 ans est estimée à 114
009.86 F[3].
Pour obtenir un intervalle de confiance de cette moyenne, il ne suffit pas de tenir compte de l’écart type de la variance résiduelle : les estimations b et a dépendent elles-même du hasard, et il est indispensable d’en tenir compte dans les calculs.
La variance de la prévision de la moyenne pour x fixé est égale à :
|
|
|
|
|
1 |
|
(x – mx)2 |
|
|
vy |
= |
s'2 |
[ |
––– |
+ |
––––––– |
] |
|
|
|
|
|
n |
|
n sx2 |
|
intervalle de
confiance de la moyenne pour x fixé :
|
[ b x + a - ta [vy ]1/2, b x + a + ta [vy ]1/2 ] |
où ta est choisi dans la table de la loi de Student en fonction du niveau de confiance 1 - a et du degré de liberté n = n – 2 et vy est donné par la formule précédente.
Exemple
: l’intervalle de confiance
de la moyenne des revenus des clients de 40 ans pour un niveau de confiance de
95% est égal à :
[ 107 267.97, 120 751.74 ]
L’estimation de la moyenne des y pour x fixé n’est pas toujours suffisante : on peut se demander entre quelles limites varient les valeurs de la variable y elle-même.
intervalle
de confiance d’une valeur individuelle:
|
[ b x + a - ta [vy’]1/2, b x + a + ta [vy’]1/2 ] |
où ta est choisi dans la table de la loi de Student en fonction du niveau de confiance 1 - a et du degré de liberté n = n – 2 et vy’ est égal à :
|
|
|
|
|
1 |
|
(x – mx)2 |
|
|
|
|
vy’ |
= |
s'2 |
[ |
––– |
+ |
––––––– |
] |
+ |
s’2 |
|
|
|
|
|
n |
|
n sx2 |
|
|
|
Exemple : l’intervalle de confiance des revenus des clients de 40 ans pour un niveau de confiance de 95% est égal à :
[ 68 440.74, 159 578.97]
Remarque : les variances précédentes montrent que les prévisions sont d’autant plus précises que la valeur fixée x est proche de la moyenne mx. Inversement, plus cette valeur s’écarte de mx, plus les prévisions sont imprécises.
On notera aussi que la prévision n’a de sens que si la liaison est linéaire, ce qui limite le champ de la prévision. Effectuer une prévision en dehors du champ à l’intérieur duquel le modèle est valide peut aboutir à des erreurs importantes.
Exemple : on ne peut pas prévoir le revenu des personnes de plus de 60 ans à
l’aide de la formule précédente puisqu’elles ont été éliminées des données de
façon que la liaison soit linéaire. Mais le calcul numérique est tout à fait
possible. On obtient, pour la moyenne d’âge des 3 clients éliminés (63 ans et
demi), un revenu moyen estimé égal à 181594.98 et un intervalle de confiance [
156 878.55, 206 311.40 ]. La moyenne des revenus de ces 3 clients, my3
= 78 777.34, est visiblement loin d’appartenir à cet intervalle de confiance :
cette erreur est due à l’application du modèle en dehors de son champ de
validité.
6. Introduction a la régression linéaire multiple
6.1
Modèle linéaire multiple.
La régression linéaire simple que nous avons présentée dans les paragraphes précédents peut être généralisée en considérant plusieurs variables explicatives X1, X2, …, Xp de la variable expliquée Y. Le modèle est alors le suivant :
|
Y = b0 + b1 X1
+ b2
X2 + … + bp
Xp + e |
La terminologie et les notations sont identiques à celles que nous avons employées en régression linéaire simple. Les coefficients b1, b2, …, bp sont les coefficients de régression théoriques, la v.a. e est la variable résiduelle. La seule différence dans la notation est celle du coefficient constant noté ici b0.
Remarque : on peut considérer comme variables explicatives les puissances successives d’une variable X. Le modèle obtenu est appelé modèle polynomial. Il est de la forme :
Y = b0 + b1 X + b2 X2 + … + bp Xp + e
Il est fréquent, pour simplifier les notations, d’introduire une variable explicative supplémentaire X0, qui est constante et égale à 1. On peut alors écrire :
|
|
|
p |
|
|
|
|
Y |
= |
S |
bj Xj |
+ |
e |
|
|
|
j = 0 |
|
|
|
Soit, pour chaque unité statistique :
|
|
|
p |
|
|
|
|
y(i) |
= |
S |
bj xj(i) |
+ |
e(i) |
|
|
|
j = 0 |
|
|
|
Le critère utilisé pour calculer les estimations bj est le même que précédemment : on cherche les valeurs b0, b1, ..., bj, ..., bp telles que l’ajustement soit le meilleur possible au sens des moindres carrés. On minimise donc la somme S :
|
|
|
n |
|
p |
|
|
|
S |
= |
S |
[ y(i) – |
S |
bj xj(i) |
]2 |
|
|
|
i = 1 |
|
j = 0 |
|
|
La régression linéaire simple apparaît comme un cas particulier de la régression linéaire multiple, avec p = 1. On peut considérer aussi que la régression simple par Xj est une régression multiple avec une contrainte sur les coefficients, dont tous sont nuls sauf les coefficients b0 et bj.
La valeur minimale obtenue sans contrainte est toujours inférieure à celle que l’on obtient sous contrainte. La somme des carrés des résidus est donc toujours inférieure ou égale à celle que l’on obtient en effectuant une régression par une seule variable, ou même plusieurs, extraites de la liste des variables Xj. Mais cela ne signifie pas que le modèle soit meilleur au plan statistique.
Les calculs sont toujours effectués par ordinateur[4]. Nous ne donnerons que les définitions et formules[5] utiles pour le choix et l’interprétation du modèle.
· le coefficient de corrélation linéaire est appelé coefficient de corrélation multiple et est noté R. C’est le coefficient de corrélation entre la variable expliquée Y et son estimation par le modèle. Il est toujours positif et son carré R2 est appelé coefficient de détermination.
· la variance des résidus est notée S2. Comme nous l’avons expliqué, lorsque toutes les variables sont prises en compte, elle est minimale, c’est-à-dire inférieure à la variance des résidus calculée à partir de variables explicatives sélectionnées parmi les précédente. On a comme précédemment :
S2 = (1 – R2) sy2
· l’estimation sans biais de la variance résiduelle S’2 est égale à :
|
|
|
n |
|
|
S’2 |
= |
––––––––– |
S2 |
|
|
|
(n – p – 1) |
|
On constate donc que le nombre p de variables explicatives intervient de deux façons différentes dans l’estimation sans biais de la variance résiduelle. Augmenter la valeur de p fait diminuer la valeur de S2, mais accroît celle du facteur n/(n – p – 1). Qu’en est-il du produit ? On ne peut donner de réponse générale, et dans certains cas, augmenter le nombre de variables explicatives se révèle néfaste au plan de la qualité de l’ajustement dans la population entière.
Exemple
: nous avons effectué la régression linéaire multiple du revenu
des clients d’Euromarket en considérant comme variables explicatives l’âge, le
montant des achats et le nombre d’enfants. Les résultats sont les
suivants :
|
Régression |
Coefficient R |
variance des résidus |
variance résiduelle sans biais |
|
multiple |
0.4926 |
44. 37 x 107 |
48.50 x 107 |
|
simple |
0.4527 |
47.86 x 107 |
49.99 x 107 |
Revenu » 2727.39 âge + 5.0547 achats + 5478.49 enfants – 8331.07
La régression linéaire multiple est meilleure que la régression linéaire simple puisque la variance résiduelle sans biais est inférieure.
6.2 Applications aux modèles économétriques
Dans les modèles économétriques, les variables considérées ne sont pas nécessairement des variables statistiques, c’est-à-dire des mesures sur un échantillon d’une même grandeur. Le temps intervient souvent, de différentes façons lorsque la variable expliquée est échelonnée dans le temps.
6.2.1 Variables explicatives de la forme Xj = tj.
On peut considérer comme variables explicatives les variables de la forme t, t2, t3, …, tp, où t représente l’instant de l’observation de la variable expliquée yt.
. Le modèle est alors le suivant :
|
|
p |
|
|
|
Yt = b0 + |
S |
bj tj |
+ e |
|
|
j = 1 |
|
|
Un certain nombre de
précautions sont ici indispensables :
· des problèmes de calcul numériques se présentent systématiquement si la variable t prend de grandes valeurs. On a tout intérêt à commencer systématiquement à la valeur t = 1, et non t = 1997 par exemple. Cette précaution est d’autant plus importante que la puissance de t considérée est élevée. Pour t = 10, on a ainsi t4 = 10 000. Il existe une procédure de calcul spécifique, fondée sur les polynômes orthogonaux. Mais dans tous les cas, les résultats numériques sont sujets à caution lorsque les calculs ne sont pas effectués en double précision.
·
on cherche
toujours la plus petite valeur possible de l’exposant p. On montre en effet
que, par n+1 points, il existe toujours un polynôme de degré n passant
exactement par ces n points (par deux points , il passe une droite).
L’ajustement de n+1 points par un polynôme de degré n ne présente donc aucun
intérêt, pas plus que de dire que deux points sont alignés.
Exemple : on considère la consommation
de viande Yt aux États-Unis de 1919 à 1941. nous disposons donc de 23
points et le temps t varie donc de t = 1 à t = 23. On peut ajuster cette série
par un polynôme de degré 3 :
Yt = b0
+ b1 t + b2
t2 + b3 t3 + et
Les
résultats numériques sont les suivants (Bensaber et Bleuse-Trillon,
1989) !:
Yt = 160.8636 + 5.6679 t - 0.7235 t2 + 0.0221 t3
+ et
avec :
·
coefficient de corrélation multiple R = 0.819
·
estimation sans biais de la variance résiduelle s’2
= 23.75
On trouvera une représentation graphique de
la série observée et de la série ajustée danas l’ouvrage de Bensaber et
Bleuse-Trillon (p. 150).
6.2.2 Variables explicatives de la forme Xj = Yt-j.
Le temps intervient par le décalage considéré par rapport à l’observation de Yt. On cherche à expliquer Yt par les valeurs observées précédentes, jusqu’à un certain rang, et le modèle est le suivant :
|
|
p |
|
|
|
Yt = b0 + |
S |
bj Yt-j |
+ et |
|
|
j = 1 |
|
|
On parle ici d’autorégression. Les problèmes fondamentaux de ce modèle concernent le choix des variables explicatives, et en particulier la valeur maximale du décalage p considéré. On peut considérer simultanément des variables explicatives de la forme tj et Yt-j.
Exemple : les mêmes données ont été analysées
en introduisant comme variables explicatives Yt-1 et Yt-2.
Yt
= b0 + b1
Yt-1 + b2 Yt-2 + et
La première observation considérée est donc Yt-2,
donc la première valeur connue est Y1 : pour calculer les
paramètres de ce modèle, il faut donc considérer t = 3, …23.
Les résultats sont les suivants :
Yt
= 59.7425 + 0.7817 Yt-1 -0.1397 Yt-2
+ et
avec :
·
coefficient de corrélation multiple R = 0.6601
·
estimation sans biais de la variance résiduelle s’2
= 42.01
6.2.3 analyse des résidus.
L’introduction du temps dans les variables observées a une conséquence importante sur les résidus. La qualité du modèle dépend des résidus, et en particulier le modèle linéaire suppose que les résidus ne sont pas corrélés deux à deux. Il faut donc vérifier cette propriété graphiquement et par des tests statistiques.
Le graphique est en général simple : on reporte simplement le temps en abscisse et les résidus en ordonnées, de la même façon que l’on représente toute série chronologique.
Les tests que l’on effectue sont classiquement un test sur le coefficient d’autocorrélation d’ordre 1, entre les séries et et et-1. Un test plus ou moins équivalent est celui de Durbin et Watson, dont une table est donnée dans un complément, et on dispose aussi d’un test « portmanteau », dont on trouvera le détail dans des ouvrages plus difficiles d’accès comme celui de Box et Jenkins.
6.3 Les conditions d’une bonne régression linéaire multiple.
Lorsque l’on dispose de plusieurs variables explicatives, il n’est pas toujours nécessaire de toutes les introduire dans le modèle linéaire. Il vaut mieux chercher parmi elles celles qui se complètent le mieux et éviter les redondances d’information qui peuvent créer ce que l’on appelle des colinéarités.
Pour mesurer cette notion d’information complémentaire, on dispose d’un coefficient appelé coefficient de corrélation partielle, dont l’interprétation est analogue à celle d’un coefficient de corrélation linéaire : le coefficient de corrélation partielle de Y et X2 sachant X1 mesure l’information apportée par X2 à Y après la régression de Y par X1.
La corrélation partielle peut être utilisée de différentes façons pour déterminer un ensemble de variables explicatives.
6.3.1 le meilleur ensemble possible
Certains logiciels donnent directement le meilleur ensemble de variables explicatives possible, ou un des meilleurs. L’inconvénient de ce genre de méthodes est qu’elles ne donnent pas à l’utilisateur la possibilité d’intervenir dans le choix des variables. Imaginons par exemple que les coefficients de corrélation de deux variables X1 et X2 avec la variable expliquée Y soient égaux à 0.61001 et 0.61000. Un algorithme fondé sur les valeurs numériques sélectionnera systématiquement la première, ce qui, au plan statistique, n’est guère justifié, la différence entre les coefficients de corrélation n’étant pas significative : il est souvent préférable dans ce cas-là de raisonner en fonction des connaissances sur les données que l’on a par ailleurs.
En outre, le modèle obtenu n’est le meilleur que sur les données observées : rien ne prouve que sur un autre échantillon, on aurait obtenu les mêmes variables explicatives. La stabilité du modèle n’est pas assurée.
6.3.2 algorithme ascendant.
· on choisit comme première variable explicative celle qui minimise la somme des carrés des résidus, ou leur variance. Compte tenu de la formule de cette variance, c’est la variable dont le carré du coefficient de corrélation linéaire avec la variable expliquée est le plus proche de 1. Si deux variables ont un coefficient de corrélation avec la variable explicative très proche l’un de l’autre, on pourra examiner les représentations graphiques des couples ou tenir compte de la nature des données.
· on définit ensuite comme deuxième variable explicative celle qui apporte l’information complémentaire la plus importante. Cette information est évaluée par le coefficient de corrélation partielle, et le raisonnement tenu sur les valeurs numériques est le même que précédemment.
· on continue cette démarche jusqu’à ce que l’information complémentaire apportée soit non significative, par un test du F sur le coefficient de corrélation partielle.
6.3.3 algorithme descendant.
La procédure est l’inverse de la précédente.
· on effectue la régression par la totalité des variables explicatives disponibles. On obtient ainsi le coefficient de corrélation multiple le plus élevé possible, mais le nombre de variables explicatives est élevé et l’estimation sans biais de la variance résiduelle n’est nécessairement minimale.
· on considère les variables explicatives dont le coefficient de corrélation partielle avec la variable expliquée conditionnellement aux autres n’est pas significatif. Parmi elles, on élimine celle dont le coefficient de corrélation partielle est le plus petit en valeur absolue.
· on effectue la régression avec les variables explicatives sauf celle qui été éliminée, et on recommence la procédure d’exclusion.
· on continue cette démarche jusqu’à ce que le coefficient de corrélation partielle de toutes les variables explicatives restantes avec la variable expliquée soit significatif.
6.3.4 algorithme stepwise.
La procédure consiste à introduire et à exclur des variables explicatives.
· l’introduction d’une variable explicative est effectuée suivant l’algorithme ascendant.
· après chaque introduction, on effectue l’algorithme descendant pour exclure une variable dont le coefficient de corrélation partielle serait devenu non significatif.
Cet
algorithme, comme les deux précédents, ne donne pas nécessairement le meilleur système possible de variables
explicatives. Sa convergence (la fin des calculs) n’a d’ailleurs jamais été
montrée dans le cas général. Il est toutefois l’un des plus utilisés.
Exemple : les coefficients de corrélation entre les quatre variables considérés sont donnés dans la matrice ci-dessous :
|
|
âge |
achat |
enfants |
revenu |
|
âge |
1.000 |
|
|
|
|
achat |
-0.055 |
1.000 |
|
|
|
enfants |
0.181 |
0.645 |
1.000 |
|
|
revenu |
0.673 |
0.115 |
0.317 |
1.000 |
Le risque de première espèce est fixé à 10%. On introduit tout d’abord la variable âge, dont le carré du coefficient de corrélation (0.6732) est le plus grand, et significatif.
On mesure ensuite l’information complémentaire apportée par les autres variables, en calculant par ordinateur les coefficients de corrélation partielle :
|
|
achat |
enfants |
|
Revenu |
0.205 |
0.267 |
On constate que c’est la variable enfants qui complète le mieux l’âge. On effectue un test sur ce coefficient de corrélation partielle : sa probabilité critique est égale à 0.069, ce qui signifie qu’avec un risque de première espèce a = 0.1, il caractérise une information significative du nombre d’enfants sur le revenu en complément de l’âge. On introduit donc le nombre d’enfants parmi les variables explicatives.
On continue l’analyse en calculant le coefficient de corrélation partielle entre le revenu et le montant des achats connaissant l’âge et le nombre d’enfants. On obtient 0.038. La probabilité critique est égale à 0.8014 : le montant des achats n’est pas utile dans le modèle de régression.
Comparons maintenant le modèle partiel (variables explicatives : âge, nombre d’enfants) au modèle complet (variables explicatives : âge, nombre d’enfants, achats) :
|
|
Coefficient R2 |
écart-type résiduel sans biais |
|
Modèle partiel |
0.4919 |
47.47 x 107 |
|
Modèle complet |
0.4926 |
48.50 x 107 |
Le modèle partiel est meilleur que le modèle complet : la
diminution du coefficient de détermination est compensée par le plus petit nombre
de variables explicatives qui intervient dans le calcul de l’écart type
résiduel sans biais. La répartition des résidus est plus proche de la loi
normale que les précédents (nous laissons au lecteur le soin de le vérifier).
Le modèle final est donc :
Revenu » 2719.9838 âge + 6234.7837 enfants – 7106.6835
CONCLUSION.
La régression linéaire est une des méthodes statistiques les plus utilisées, et la facilité avec laquelle les logiciels ou les calculatrices donnent l’ensemble des résultats fait souvent négliger la vérification des hypothèses indispensables à la validité du modèle. Prévoir par exemple le chiffre d’affaires d’une entreprise en ajustant une droite aux chiffres réalisés les quatre ou cinq années précédentes n’a aucune valeur statistique.
Précisons aussi que les notions de cause et d’effet résultent d’une analyse qui n’a rien de statistique : c’est un choix que l’utilisateur doit effectuer par une approche de nature différente, par une analyse économique ou psychologique par exemple, et la régression consiste à décrire cette relation mais ne peut ni l’inverser ni la justifier.
D’autres méthodes de régression existent, dont nous n’avons pas parlé, en particulier la régression non linéaire, qu’il ne faut pas confondre avec la régression polynomiale. Ces méthodes sont beaucoup trop difficiles pour figurer dans cet ouvrage. On trouvera dans les applications pédagogiques de ce chapitre une introduction à la régression bornée (ou ridge regression) et à la régression sur composantes principales.
TABLE DES MATIERES
1. Modèle de régression simple.
1.1 Variable explicative et variable expliquée.
2. Nature de
la liaison. graphiques.
2.2 Représentation graphique et courbe de régression.
3.1 Critère des moindres carrés
3.2 Estimation des coefficients de régression.
5.1 Estimation et intervalle de confiance de la variance résiduelle.
5.2 Test sur les coefficients de régression.
5.3 Prévision ponctuelle et par intervalle de confiance.
6.
Introduction a la régression linéaire multiple
6.2 Applications aux modèles économétriques
6.2.1 Variables explicatives de la
forme Xj = tj.
6.2.2 Variables explicatives de la
forme Xj = Yt-j. 25
6.3 Les conditions d’une bonne régression linéaire multiple.
6.3.1 le meilleur ensemble possible
