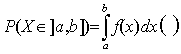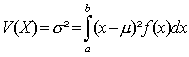notions de probabilités

Les chapitres précédents donnent des méthodes graphiques et numériques pour caractériser les principales propriétés d’un ensemble de données.

Cet ensemble de données est constitué, dans certains cas, d’observations tirées au hasard au sein d’une population, par exemple dans un fichier informatique. Avant d’étendre les propriétés observées sur cet ensemble à la totalité de cette population, il faut tenir compte du fait que ces propriétés dépendent du tirage effectué : un autre tirage au hasard ne donnera peut-être pas les mêmes résultats. Pour cela, il est nécessaire de connaître les notions élémentaires de la théorie des probabilités que nous présentons dans ce chapitre.

1. Probabilités. probabilités conditionnelles.

1.1 Population et événements.

Les définitions données ci-dessous établissent en fait une équivalence entre le langage des probabilités et le langage de la théorie des ensembles. Nous utiliserons dans la suite ces deux langages suivant le contexte.

Définitions :

· On appelle population statistique un ensemble W constitué de N éléments appelés unités statistiques (notées u.s.) ou individus. Le nombre N est appelé nombre de cas possibles.

· On appelle événement un sous-ensemble de la population W. Le nombre N_A d’u.s. appartenant à un événement A est appelé « nombre de cas favorables ».

Cette population est celle dans laquelle on effectuera ultérieurement des tirages au hasard, et nous serons parfois amenés à la considérer comme infinie, de même que le nombre d’u.s. appartenant à un événement. Elle est souvent appelée urne en probabilités.

Nous dirons que l’événement A s’est réalisé si l’unité statistique tirée au hasard appartient au sous-ensemble A.

Relations et opérations :

On considère deux sous-ensembles A et B de W.

· Il existe deux événements très particuliers :

§ L’événement certain caractérisé par la population W.

§ L’événement impossible ou ensemble vide noté par la lettre grecque F (phi).

· On dit que B est inclus dans A si tous les éléments de B appartiennent à A (figure 1).

L’inclusion signifie en particulier que si B est inclus dans A, la réalisation de l’événement B, définie par le tirage d’un élément de B, entraîne la réalisation de l’événement A puisque l’élément tiré, s’il appartient à B, appartient aussi à A.

Réciproquement, si la réalisation de B entraîne toujours celle de A, tout élément de B appartient à A et le sous-ensemble B est inclus dans le sous-ensemble A.

· L’ensemble « A inter B » ou événement « A et B » noté AÇB, est constitué des éléments qui appartiennent à la fois à A et à B.

· L’ensemble « A union B » ou événement « A ou B » noté AÈB est constitué des éléments de A, de B ou de A et B (figure 2). On dit que le « ou » est inclusif.

On a donc la relation suivante : [AÇB] Ì [AÈB].

· le sous-ensemble complémentaire d’un sous-ensemble B (figure 4) est défini par le sous-ensemble A tel que :

AÈB = W

AÇB = F.

On note alors : A = B^c

Le complémentaire de A = B^c est évidemment A^c = B. La population W et l’ensemble vide F sont complémentaires.

1.2 Définition et propriétés des probabilités.

On considère une population W d’effectif N et un événement A d’effectif N_A.

Définition : on appelle probabilité de l’événement A le rapport N_A/N.

La probabilité N_A/N est égale à ce que l’on appelle couramment « le rapport du nombre de cas favorables N_A au nombre de cas possibles N ».

Cette notion de probabilité est appelée équiprobabilité : la probabilité d’un événement constitué d’une seule unité statistique est constante et égale à 1/N.

Définition : Tirages avec et sans remise :

· L’unité statistique tirée peut être remise dans la population et être éventuellement retirée : le tirage est dit indépendant puisqu’il n’exerce aucune influence sur les tirages suivants.

· Inversement, si l’u .s. n’est pas remise, les nombres N_A et N sont diminués de 1 : après le premier tirage, la probabilité de l’événement A devient (N_A – 1)/(N – 1) et n’est plus la même : les tirages sont « dépendants » ou « sans remise ».

Propriétés des probabilités :

· La probabilité est un nombre compris entre 0 et 1 :

0 £ P(A) £ 1

Cette propriété est évidente, le nombre de cas favorables étant toujours positif ou nul et inférieur ou égal au nombre de cas possibles.

· La probabilité de la population W est égale à 1 et celle de l’ensemble vide F à 0 :

P(W) = 1

P(F) = 0

Lorsque l’événement est la population W, les cas favorables sont les cas possibles : il y a égalité des effectifs, et lorsque c’est l’ensemble vide F, le nombre de cas favorables est nul.

· La probabilité de l’événement complémentaire est égale à :

P(A^c) = 1 – P(A)

Les éléments de A^c sont ceux qui n’appartiennent pas à A. Il y en a donc N – N_A, d’où la relation.

· La probabilité de l’union de deux événements est donnée par :

P(AÈB) = P(A) + P(B) – P(AÇB)

Les éléments de A È B sont les éléments de A (il y en a N_A), les éléments de B (il y en a N_B). En ajoutant N_A et N_B, on compte deux fois les éléments qui appartiennent à la fois à A et à B, c’est-à-dire de AÇB : il est donc nécessaire de les soustraire une fois. D’où la relation précédente dite « additivité forte ».

· Si un sous-ensemble B est inclus dans un sous-ensemble A, la probabilité P(B) est inférieure ou égale à la probabilité P(A)

B Ì A

P(B) £ P(A)

C’est une conséquence directe de la définition de l’inclusion : tous les éléments de B appartiennent à A : le nombre d’éléments de B est inférieur ou égal au nombre d’éléments de A et par suite le rapport N_B/N est inférieur au rapport N_A/N.

Définition généralisée d’une probabilité et d’un espace probabilisé :

Il n’est pas toujours possible de définir la population, les événements et les probabilités comme précédemment, en particulier dans le cas où la population est infinie, comme par exemple un ensemble de nombres. Pourtant, il est naturel de considérer que si l’on tire au hasard un nombre entier, il y a une chance sur deux d’obtenir un nombre pair, une chance sur trois un nombre divisible par trois … On est donc amené à généraliser les définitions précédentes de la façon suivante :

· un univers est un ensemble quelconque W.

· les événements sont des sous-ensembles de W tels que l’union d’événements, l’intersection et la complémentation sont des événements.

· la probabilité est une application qui à tout événement A associe un nombre P(A) vérifiant les propriétés précédentes.

La formalisation de la population considérée est parfois complexe. Elle est rarement indispensable, et souvent il n’est pas indispensable d’en donner la définition précise. Dans toute la suite du chapitre, les propriétés seront explicitées dans le cas de la définition initiale de la probabilité (rapport du nombre de cas favorables au nombre de cas possibles).

1.3 Indépendance et probabilité conditionnelle.

La formule de Bayes (18^e siècle) permet de prendre en compte la réalisation d’un événement pour réévaluer la probabilité d’un autre. Par exemple, la réalisation de l’événement A : « la personne est de sexe féminin » a un impact évident sur la probabilité de l’événement B : « la personne chausse du 41», peu de femmes chaussant du 41.

Considérons deux événements A et B, d’effectifs N_A et N_B. On note N_A_ÇB l’effectif du sous-ensemble AÇB. Dans l’exemple précédent, AÇB est l’ensemble de femmes chaussant du 41 et N_A_ÇB leur nombre.

Supposons que l’événement A soit réalisé : on a donc tiré un élément parmi les N_Aéléments de A. Examinons ensuite la probabilité de B : elle est maintenant définie par le rapport N_A_ÇB/N_A:

N_A_Ç_B		N_A_Ç_B		N_A
^________	=	^_______	/	^____
N_A		N		N

Définition : La probabilité conditionnelle d’un événement B pour un événement A fixé de probabilité non nulle est définie de la façon suivante :

P(B/A) = P(BÇA)/P(A)

La probabilité de B n’a pas changé si l’on a :

N_A_Ç_B		N_B
^_______	=	^____
N_A		N

Cette relation peut s’écrire de la façon suivante :

N_A_Ç_B		N_A		N_B
^________	=	^_____	x	^_____
N		N		N

Définition : on dit que deux événements A et B sont indépendants quand la réalisation de l’un ne modifie pas la probabilité de l’autre.

Propriété caractéristique : deux événements A et B sont indépendants si et seulement si la probabilité de l’événement A Ç B est égale au produit des probabilités :

P(AÇB) = P(A) P(B)

Exemple : on lance un dé à 6 faces. On étudie les événements A : le chiffre obtenu est pair, B : le chiffre obtenu est inférieur ou égal à 3, C : le chiffre obtenu est 1, 3, 4 ou 6.

On a : P(A) = 1/2 P(B) = 1/2 P(C) = 2/3

A Ç B: le chiffre obtenu est pair et compris entre 1 et 3, donc c’est 2 : P(A Ç B) = 1/6.

P(A) P(B) = 1/4 : A et B ne sont pas indépendants.

A Ç C : le chiffre obtenu est 4 ou 6 : P(A Ç C) = 2/6

P(A) P(C) = 2/6 : A et C sont indépendants.

Calculons les probabilités conditionnelles :

P(B/A) = P(A Ç B)/P(A) = (1/6 ) / (1/2) = 1/3¹ P(B) = 1/2

P(C/A) = P(A Ç C)/P(A) = (2/6 ) / (1/2) = 2/3= P(C) = 2/3

Formule de Bayes : soit A un événement de W. On considère un événement B et son complémentaire B^c . On a :

		P(A/B) P(B)
P(B/A)	=	^{___________________________________}
		P(A/B) P(B) + P(A/B^c) P(B^c)

La démonstration de cette formule est donnée dans les compléments.

Exemple : il y a une femme sur deux adultes dans la population française, et, parmi les femmes, une sur dix chausse du 41, la proportion étant de un sur cinq chez les hommes. Calculons la probabilité qu’une personne chaussant du 41 soit une femme.

On note A l’événement « la personne chausse du 41 », B l’événement « la personne est une femme » et évidemment B^c l’événement « la personne est un homme ». On a donc :

P(B) = 1/2	P(B^c) = 1/2
P(A/B) = 1/10	P(A/B^c) = 1/5

On en déduit :

		(1/10) x (1/2)		1
P(B/A)	=	^{_________________________________}	=	^____
		(1/10) x (1/2) + (1/5) x (1/2)		3

2. Variables aléatoires. lois de probabilité.

2.1 Variables aléatoires

Définition : on appelle variable aléatoire (notée v.a.) une application qui à chaque u.s. tirée au hasard dans W associe un objet ou un nombre appartenant à un ensemble V.

X :

^______>

· La v.a. X est appelée discrète si l’ensemble V est inclus dans l’ensemble des entiers N (ou si elle prend un nombre fini de valeurs x₁, x₂, …, x_n).

· La v.a. X est appelée continue si l’ensemble V est égal à l’ensemble des réels R ou à un intervalle de R. Nous apporterons des précisions ultérieurement.

· La v.a. X est appelée qualitative si l’ensemble V est un ensemble de modalités (par ex. la liste des couleurs des cheveux, des catégories socioprofessionnelles, etc.)

Exemple : on considère les variables aléatoires définies sur l’ensemble de la clientèle d’E UROMARKET suivantes :

l’âge X₁,	le nombre d’enfants X₂,
le revenu X₃,	la catégorie socioprofessionnelle X₄,
le montant de ses achats X₅.	le sexe X₆.

L’âge, le revenu, le montant des achats définissent des variables aléatoires quantita tives ; ce sont des variables aléatoires « réelles », dont les valeurs appartiennent à l’ensemble R des nombres réels.

X₁, X₃, X₅ :

^______>

V = R

Le sexe et la catégorie socioprofessionnelle définissent des variable aléatoires qualitatives dont les modalités sont pour le sexe F pour Féminin et M pour Masculin et pour la catégorie socioprofessionnelle :

Agri : agriculteur ; ouvrier agricole	C.M. : cadre moyen ;
Ouv. : ouvrier	C.Sup. : cadre supérieur;
Emp. : employé ;	PIC : Commerçants, artisans ;
	Inact. : inactifs, retraités, chômeurs, étudiants .

Le nombre d’enfants est une variable aléatoire discrète puisqu’elle prend les valeurs 0, 1, 3, .... La notion de moyenne ayant un sens, c’est une variable quantitative.

2.2 Probabilité d’un intervalle.

Soit X une v.a. et I un sous-ensemble de V. On appelle événement « XÎ I » l’ensemble A des u.s. u de la population telles que X(u) Î I.

On note N_A le nombre d’unités statistiques de A. On a donc :

P [XÎI] = N_A/N

Chaque variable aléatoire X « transporte » donc la probabilité P définie sur la population statistique W sur l’ensemble X(W ), en général l’ensemble des nombres réels R (figure 5.4) . Cette probabilité transportée est notée fréquemment P_X.

Définition : on appelle loi de probabilité de la variable X la probabilité définie sur W transportée par X sur R.

Exemple : On considère l’âge (v.a. X₁) : . L’événement 33£ X₁£ 45 est défini par l’ensemble A des clients âgés de 33 à 45 ans. La probabilité P(33£ X₁£ 45) est égale par définition à la probabilité P(A), c’est-à-dire à la proportion de clients âgés de 33 à 45 ans dans la population totale.

On considère le sexe (v.a. X₆). L’événement {X₆ = F} est défini par l’ensemble B des clients de sexe féminin. La probabilité P(X₆= F) est égale par définition à P(B), c’est-à-dire à la proportion de clientes dans la population totale.

2.3 Loi de probabilité d’une v.a. discrète.

Définition : la densité de la loi probabilité (ou densité de probabilité) d’une v.a. dis c rète dont les valeurs possibles sont x₁, x₂, ..., x_i, ..., …x_i, …, x_n est définie par la suite de toutes les probabilités p_i = P(X = x_i), i = 1, …, n.

Dans le cas où il existe une infinité de valeurs possibles de la v.a. X, on supposera que les sommes de 1 à n données ci-dessous tendent vers une limite lorsque n tend vers l’infini ; la notation consiste simplement à remplacer n par + ¥.

Exemple : on considère la variable définie par le nombre d’enfant. Sa loi de probabilité est la suite p₀, p₁, p₂, ... définie par :

p₀ = nombre de clients sans enfant / nombre total de clients

p₁ = nombre de clients ayant 1 enfant / nombre total de clients

p₂ = nombre de clients ayant 2 enfants / nombre total de clients

etc.

Propriétés :

· la probabilité P[XÎ{x₁, x₂, ..., x_l}] est la somme des probabilités P[ X = x₁], P[ X = x₂], ..., P[ X = x_l] :

P[ X Î{x₁, x₂, ..., x_l}]= P[ X = x₁] + P[ X = x₂] + ... + P[ X = x_l]

· la somme de toutes les probabilités p_i est égale à 1 :

		n
p₁ + p₂ + p₃ + ... p_i + … + p_n	=	S	p_i	=	1
		i = 1

Ces propriétés découlent directement de la définition de la probabilité par le rapport du nombre de cas favorables au nombre de cas possibles.

Définitions :

· l’espérance E(X) (ou moyenne m) d’une v.a. discrète prenant les valeurs x₁, x₂, ..., x_i, ..., x_n est la somme ci-dessous :

m = E(X) = p₁ x₁ + p₂ x₂ + ... p_i x_i + … p_n x_n

Soit :

		n
m = E(X)	=	S	p_i x_i
		i = 1

· la variance V(X) (ou s²) d’une v.a. discrète prenant les valeurs x₁, x₂, ..., x_i, ..., x_n est la somme ci-dessous :

s²= V(X)		= p₁ (x₁ – m)² + p₂ (x₂ – m)^{2 +}... + p_i (x_i – m)² + ... + p_n (x_n – m)²
			n
s² = V(X)	=		S	p_i (x_i – m)²
			i = 1

On montre que cette variance est égale à

s² = p₁ x₁² + p₂ x₂² + ... + p_i x_i² + … + p_n x_n² – m²

		n
s² = V(X)	=	S	p_i x_i² – m²
		i = 1

c’est-à-dire à l’espérance des carrés moins le carré de l’espérance.

Le terme s est appelé écart-type.

· La fonction de répartition théorique est une fonction définie pour toute valeur réelle x par la relation ci-dessous :

F(x) = P(X £ x)

Remarque : nous retrouvons les définitions déjà vues de la moyenne, de la variance et de la fonction de répartition d’une série d’observations, mais ici il s’agit de valeurs théoriques, concernant une variable aléatoire, et non une suite de valeurs observées. La statistique consiste justement à trouver des valeurs approchées de ces paramètres et de la fonction, les meilleures si possible, et à en étudier les propriétés.

2.4 Loi de probabilité d’une v.a. continue.

On considère une v.a. continue X. Nous allons définir la densité de la loi de probabilité de cette variable en plusieurs étapes. On définit tout d’abord des intervalles disjoints recouvrant l’ensemble des valeurs possibles de la variable X : I₁, I₂, ..., I_i..., I_k.

On en déduit les probabilités P₁, P₂,..., P_i, ...P_k :

P_i = P(XÎI_i)

Densit é par intervalle :

On appelle densité par intervalle définie sur k intervalles I_i, i = 1, …, k la suite (d_i) i = 1, …, k définie par :

d_i = P_i/l_i

où l_i est l’amplitude de l’intervalle I_i.

Relation fondamentale : P_i = d_i x l_i

Remarque : en supposant que la population est d’effectif fini N, les probabilités P₁, P₂,..., P_i, ...P_k sont définies de la façon suivante :

P_i = P(XÎI_i) = N_i/ N

et la densité par intervalle de l’intervalle I_i de longueur l_i par :

d_i = ( N_i / N) / l_i

La notion de densité par intervalle d’une variable aléatoire est donc la même que celle que nous avons définie dans le chapitre 1 pour construire des histogrammes. Mais la densité est ici calculée à partir des probabilités et non des proportions.

Exemple : on considère la variable montant des achats que l’on suppose toujours compris entre 0 et 1000F. On définit les intervalles :

I₁ = [0, 200[	I₂ = [200, 500[
I₃ = [500, 800[	I₄ = [800, 1000]

On suppose N = 15 000, N₁ = 3000, N₂ = 4700, N₃ = 4400, N₄ = 2900.

On en déduit la densité par intervalle :

d₁ = 0.0010	d₂ = 0.001044
d₃ =0.000978	d₄ = 0.000967

Définition : on appelle densité de probabilité d’une variable continue la fonction f(x) limite de la densité par intervalle lorsque le nombre d’observations augmente indéfiniment et que la longueur des intervalles tend vers 0.

Cette définition repose sur l’hypothèse de la convergence du rapport P_i/l_i dont le numérateur P_i =N_i/ N et le dénominateur l_i tendent vers 0. Dans le cas d’une population finie, la densité de l’intervalle I_i de centre noté x est :

d_i = ( N_i/N ) / l_i

Lorsque N tend vers l’infini et que l_i tend vers 0, le numérateur N_i/ N tend vers 0 et le dénominateur l_i aussi : la limite du rapport est indéterminée. L’hypothèse que l’on effectue pour définir les v.a. continues consiste à supposer que la limite du rapport existe, dépend du centre de l’intervalle et est donc de la forme f(x). Lorsque cette limite n’existe pas, la variable n’est pas continue : nous n’étudierons pas ce genre de variable aléatoire.

Exemple : nous considérons une population constituée de 15 000 valeurs que nous répartissons en 20 classes de même amplitude. La densité par intervalle suivant ces 20 classes est représentée par l’histogramme (figure 6). La densité théorique (ici la densité de la loi normale définie plus loin) est la courbe superposée à cet histogramme.

2.5 Propriétés et calcul des probabilités.

· L’aire comprise entre la courbe et l’axe des abscisses de –¥ à + ¥ est égale à 1. En effet, cette aire est la limite de la somme des aires des rectangles, qui est la somme des probabilités P_i, donc toujours égale à 1.

· La probabilité de l’événement { X Î [ a, b] } (ou { X Î [ a, b [ } ) est égale à l’aire comprise entre la densité, l’axe des abscisses et les droites x = a et x = b. Une approximation de cette aire est donnée par l’aire du rectangle défini par l’intervalle [a, b] et la densité dans cet intervalle (figure 6).

· On définit l’espérance et la variance en considérant la densité par intervalle. Pour des intervalles I_i fixés, on peut calculer l’espérance et la variance comme dans le cas des variables aléatoires discrètes. En nous limitant à la notion d’espérance (le raisonnement est identique dans le cas de la variance), on étudie la somme :

	n
p₁ x₁ + p₂ x₂ + ... p_i x_i + … p_n x_n =	S	p_i x_i
	i = 1

Lorsque la longueur des intervalles I_i tend vers 0 et que le nombre d’observations augmente indéfiniment, le nombre n tend vers l’infini et les probabilités p_i deviennent égales aux produits f(x_i) l_i par définition de la densité f(x). L’espérance est alors la limite de la somme ci-dessus.

Ces propriétés s’expriment de façon simple par le calcul intégral élémentaire.

· La probabilité de l’événement { X Î ] a, b] } est l’intégrale de la densité définie entre x = a et x = b.

· L’intégrale entre – ¥ et + ¥ est égale à 1.

· Cette intégrale est égale à F(b) – F(a), où F(x) est une primitive de la densité f(x) (ou la dérivée de F(x) est égale à la densité f(x)).

· L’espérance et la variance sont définies de la façon suivante :

· La fonction F(x) définie par la relation ci-dessous :

F(x) = P(X £ x)

est appelée fonction de répartition de la v.a. Sa dérivée est égale à la densité f(x). On a :

P(a < X £ b) = F(b) – F(a)

La démarche pratique ne fait presque jamais appel au calcul intégral. Dans la quasi totalité des cas en effet, F(a) et F(b) sont donnés dans une table numérique ou calculés par ordinateur (on en trouvera des exemples dans le paragraphe ci-dessous).

Pour calculer les probabilités d’événements dans le cas d’une v.a. continue, on utilise les propriétés suivantes :

· P( XÎ ] a, b ]) = P( XÎ [ a, b [ ) = P( XÎ ] a, b [ ) = P( XÎ [ a, b ])

· Soit c Î ] a, b[ : P( XÎ [ a, b ]) = P( XÎ [ a, c [ ) + P( XÎ [ c, b [ )

· P( XÎ ] – ¥, a ]) = F(a)

· P( XÎ ] a, + ¥ ]) = 1 – F(a)

Pour calculer l’espérance et la variance des v.a., on utilise les propriétés suivantes :

· E(a X + b Y ) = a E(X) + b E(Y)

· V(a X+ b ) = a² V(X)

3. Lois de probabilité discrètes.

Les lois de probabilités discrètes présentées dans ce paragraphe sont les plus courantes. Nous les complétons en exercice par la loi géométrique et donnons les démonstrations des formules dans les compléments.

3.1 Loi uniforme discrète.

Définition : la variable X dont les valeurs possibles sont 1, 2, ..., n suit la loi uniforme discrète sur {1, 2, ..., n} si la probabilité p_i = P(X=i) est égale à 1/n quel que soit i.

Propriété : l’espérance m et la variance s² d’une variable qui suit la loi uniforme discrète sur {1, …, n} sont égales à :

	n + 1		n² – 1
m =E(X) =	–––––	s² = V(X) =	–––––
	2		12

3.2 Loi de Poisson

Définition : la loi de Poisson de paramètre l strictement positif est la loi d’une v.a. X à valeurs dans N et définie par sa densité :

		e^–^l lⁱ
p_i = P[X = i]	=	––––––––––
		1 x 2 x 3... x i

Le dénominateur de l’expression ci-dessus est le produit des n premiers nombres entiers et est appelé factorielle i. On le note i! : i! = 1 x 2 x 3... x i.

Propriété : l’espérance et la variance d’une variable qui suit la loi de Poisson de paramètre l sont égales à l :

m = E(X) = l

s² = V(X) = l

Les valeurs de la densité sont données dans la table statistique de la loi de Poisson.

Exemple : Densité de la loi de Poisson pour l = 2.

i	P(X=i)	P(X£i)	i	P(X=i)	P(X£i)
0	0.135335	0.135335	7	0.003437	0.998903
1	0.270671	0.406006	8	0.000859	0.999763
2	0.270671	0.676676	9	0.000191	0.999954
3	0.180447	0.857123	10	0.000038	0.999992
4	0.090224	0.947347	11	0.000007	0.999999
5	0.036089	0.983436	12	0.000001	1.000000
6	0.012030	0.995466	13	0.000000	1.000000

Théoriquement la v.a. peut prendre les valeurs de 0 à + ¥. Mais la probabilité p_i est quasi nulle à partir de i = 13.

On pourra vérifier par le calcul que la moyenne et la variance sont égales à 2.

C’est le cas général de toutes les v.a. discrètes prenant une infinité de valeurs : la probabilité devient très petite et quasi nulle à partir d’une certaine valeur.

3.3 Loi de Bernoulli et loi binomiale.

On considère un événement E tel que P(E) = p. On a évidemment P(E^c) = 1–p. On définit la v.a. X prenant la valeur 1 si l’événement E est réalisé, 0 sinon. La v.a. X est appelée indicatrice de E. Elle suit par définition la loi de Bernoulli de paramètre p.

Définition : on dit qu’une v.a. X suit la loi de Bernoulli de paramètre p si c’est la variable indicatrice d’un événement E de probabilité p. Elle prend les valeurs 0 ou 1 avec les probabilités suivantes :

P ( X= 0) = 1 – p

P(X = 1) = p

On a :

m = E(X) = p

s² = V(X) = p (1 – p)

Définition : on appelle variable binomiale de paramètres n et p la v.a. définie par le nombre de réalisations d’un événement de probabilité p au cours de n tirages indépendants.

Une variable binomiale peut être considérée comme la somme de n v.a. X_i indicatrices d’événements E_i indépendants et de probabilité p :

X = X₁ + X₂ + … + X_i + … + X_n

La densité de la v.a. est donnée par la formule :

	1 x 2 x 3 x .. x n
p_i = P(X = I ) =	^{_________________________________________}	(1 – p)^{n – i} pⁱ
	(1 x 2 x 3 x .. x i) x (1 x 2 x 3 x ... x [n– i])

On écrit, en utilisant la notation factorielle définie dans le paragraphe sur la loi de Poisson (on pose par convention 0! = 1, et on rappelle que x⁰ = 1 quelle que soit la valeur x) :

	n!
p_i = P(X = i ) =	^__________	(1 – p)^{n – i} x pⁱ
	i! [n– i]!

On retrouve dans cette formule le nombre de combinaisons de i éléments pris parmi n et noté C_nⁱ (un rappel d’analyse combinatoire est donné dans les compléments).

La densité de la loi binomiale B(n,p) est finalement la suivante :

quel que soit i de 0 à n

p_i = C_nⁱ (1 – p)^{n – i} x pⁱ

L’espérance et la variance sont données par les formules ci-dessous :

m = E(X) = n p

s² = V(X) = n p (1 – p)

Remarque : Les valeurs de la densité sont données dans la table statistique de la loi binomiale. Pour p = 0.3 et n = 5, on a :

i	P(X=i)	P(X£i)	i	P(X=i)	P(X£i)
0	0.168070	0.168070	3	0.132300	0.969220
1	0.360150	0.528220	4	0.028350	0.997570
2	0.308700	0.836920	5	0.002430	1.000000

Pour les valeurs de n telles que n p >5 et n (1 – p ) >5, on peut utiliser une approximation par la loi normale : la probabilité P(X = i) où X suit la loi binomiale B(n,p) a pour valeur approchée la probabilité P( i – 0.5 < Y < i + 0.5) où Y suit la loi normale de paramètre m = n p et s² = n p (1 – p). On se reportera au paragraphe 4.3.

4. Lois de probabilité continues.

Nous ne définissons ci-dessous que les lois continues les plus couramment utilisées en statistique. Les démonstrations des formules d’espérance et de variance sont données dans les compléments.

4.1 Loi uniforme continue.

Définition : la densité de la loi uniforme continue sur un intervalle ] a, b [ est définie par la fonction f(x) :

Pour x Î ] a, b[	f(x) = 1/(b–a)
Pour x £ a ou x ³ b	f(x) = 0

Les bornes a et b peuvent être incluses ou exclues de l’intervalle : elles sont de probabilité nulle et cela ne change rien.

Un exemple d’une telle variable est donné par la touche « rnd » ou « random » qui figure sur un grand nombre de calculatrices : à chaque pression de cette touche, on obtient un nombre compris entre 0 et 1, et la densité de cette variable aléatoire est la loi uniforme sur l’intervalle ] 0, 1 [.

Propriétés :

· La moyenne m et la variance s² théoriques d’une loi uniforme continue sur ] a, b [ sont égales à :

	a + b		(b – a )²
m =E(X) =	–––––	s² = V(X) =	––––––
	2		12

· La probabilité d’un intervalle [ x₁, x₂ ], avec a £ x₁£ x₂ £ b suivant la loi uniforme continue sur ] a, b [ est égale à :

P( X Î] x₁, x₂ ]) = (x₂ – x₁)/(b – a)

Exemple : on considère la loi uniforme continue sur ]0, 2[.

La densité est définie par la fonction f(x) :

pour x Î ] 0, 2[	f(x) = 1/2
pour x £ 0 ou x ³ 2	f(x) = 0

Sur la figure 7, la probabilité de l’événement X Î ] x₁, x₂ ] est l’aire du rectangle représenté en gris. Elle est égale évidemment à P (X Î [ x₁, x₂ ]).

4.2 Loi exponentielle.

La loi exponentielle est la loi de l’intervalle aléatoire séparant deux événements successifs : en cela, elle est utilisée conjointement avec la loi de Poisson pour l’analyse des files d’attente. Son expression mathématique utilise la fonction exponentielle dont une présentation est donnée dans les compléments.

Définition : on appelle loi exponentielle de paramètre a>0 et x₀ Î R la loi de probabilité dont la densité est donnée par la fonction suivante :

		_{–a (x – x0)}
pour tout x ³ x₀	f(x) = a e
pour tout x < x₀	f(x) = 0

Il n’existe pas de table statistique donnant les valeurs de la fonction de répartition F(x) dans le cas de la loi exponentielle. Une simple calculatrice suffit puisque l’on a :

		_{–a (x – x0)}
F(x) = 1 –	e

Propriété : la moyenne m et la variance s² théoriques sont égales à :

m = E(X) = x₀ + 1/a

s² = V(X) = 1/a²

Nous donnons en figure 8 la représentation graphique de cette densité pour a = 2 et
x₀= 0. La probabilité de l’intervalle [ 1, 1.5] indiqué sur la figure est l’aire de la région comprise entre les deux segments. Elle est égale à F(x₂) – F(x₁), où F est la fonction de répartition. On a donc :

		–( x₁ – x₀)		–( x₂ – x₀)
P(XÎ ] x₁, x₂] ) =	e		– e

4.3 Loi normale.

La loi normale est une densité théorique donnant la répartition d’une infinité d’observations sous la forme d’une courbe dite courbe en cloche (fig ure 9) à laquelle nous avons déjà fait référence dans les chapitres antérieurs. Elle est appelée aussi loi de Laplace-Gauss. Elle fait intervenir deux paramètres m et s (p = 3.1415…évidemment).

Définition : on appelle loi normale de paramètres m Î R et s > 0 la loi de probabilité dont la densité est définie par la fonction suivante :

	1		– ½ [ (x – m)/s ]²
f(x) =	^{_____________}	e
	s [ 2 p ]^1/2

Propriétés :

· Les paramètres m et s² sont la moyenne et la variance de la loi normale.

· Si X suit la loi normale de moyenne m et de variance s², la loi de (X – m)/s est la loi normale de moyenne 0 et de variance 1. La v.a. (X – m)/s est centrée et réduite.

Les zones grisées sur la figure 9 correspondent aux valeurs ±1.96 ; elles ont chacune pour aire 0.025, ou 2.5%. On retrouve la première règle de classification des valeurs observées proposée dans le chapitre 2 :

P[ m – 1.9600 s < X < m + 1.9600 s ]	= 0.95
P[ m – 1.6449 s < X < m + 1.6449 s ]	= 0.90
P[ m + 1.0364s < X < m + 1.0364 s ]	= 0.70
P[X < m – 1.9600s ]	= 0.025
P[X > m + 1.9600 s ]	= 0.025
P[X > m + 1.6449 s ]	= 0.050
P[X < m – 1.6449 s ]	= 0.050
P[X > m + 1.0364 s ]	= 0.150
P[X < m – 1.0364 s ]	= 0.150

L’importance de la loi normale est considérable en statistique : on la rencontre très fréquemment dans les applications et elle possède des propriétés fondamentales dont la plus importante est connue sous le nom de « theorem central limit », ou, en français, théorème de la limite centrale (on dit aussi centrée), que nous énonçons dans le chapitre suivant.

4.4 Loi du c² et loi de Fisher.

La loi du c² (du Chi²) de Pearson est la loi d’une v.a. notée souvent X² (il ne s’agit pas du carré d’une v.a. X) et définie par la somme de carrés de v.a. indépendantes suivant la loi normale centrée réduite X₁, X₂, …, X_n:

X² = X₁² + X₂² + … + X_n²

Le nombre n de ces v.a. normales et appelé degré de liberté. L’espérance de X² est égale à n et sa variance à 2 n. On notera que la densité n’est pas symétrique (figure 10).

Les zones grisées correspondent aux valeurs 31.55 et 70.22 ; elles ont pour aire 0.025 (ou 2.5%). La probabilité qu’une variable qui suit la loi du c² de degré de liberté n = 49 soit comprise entre 31.55 et 70.22 est donc égale à 0.95.

La loi de Fisher (ou Fisher Snedecor) est la loi de probabilité du rapport F de deux variables X₁² et X₂² suivant chacune la loi du c² de degré de liberté n₁ et n₂, et divisées par ces degrés de liberté :

	X₁² / n₁
F =	–––––––––
	X₂² / n₂

On notera que si F suit la loi de Fisher de degrés de liberté n₁ et n₂, 1/F suit la loi de Fisher de degrés de liberté n₂ et n₁.

Ces lois sont utilisées pour effectuer des estimations par intervalle de confiance et des tests d’indépendance (cf. paragraphe 5 .3 et chapitres suivants)

4.5 Loi de Student.

La loi de Student est la loi d’une v.a. notée T définie par le rapport d’une v.a. X suivant la loi normale centrée réduite et de la racine carrée d’une v.a. X²suivant la loi du c² et divisée par son degré de liberté :

	X
T =	––––––
	[X²/n]^1/2

Elle dépend de ce degré de liberté noté n. Elle est symétrique, de moyenne nulle, de variance n/(n – 2). Sa d ens ité (figure 11) est une fonction compliquée dont l’expression ne présente pas d’intérêt ici. Lorsque le degré de liberté n augmente (n>120), la loi de Student est confondue avec la loi normale centrée réduite.

5. Couples de variables aléatoires.

La notion de couple de variables aléatoires est indispensable pour aborder la question de l’indépendance entre deux variables qualitatives ou quantitatives. Nous nous limitons au cas de deux variables qualitatives que nous reprendrons dans le chapitre 7.

5.1 Couples de variables aléatoires qualitatives.

Nous étudions tout d’abord les couples de v.a. qualitatives, la seule difficulté venant des notations un peu compliquées.

Un couple de v.a. qualitatives est constitué de deux v.a. qualitatives observées sur une même population W . Nous noterons ici la taille de la population par la lettre minuscule n, pour conserver la notation utilisée généralement . On note :

· X la première v.a., x₁, x₂, …, x_i, …x_p ses modalités.

· Y la seconde v.a., y₁, y₂, …, y_j, …, y_q ses modalités

Le nombre de cas favorables n_i,j est le nombre d’unités statistiques vérifiant les deux modalités à la fois. La probabilité p_i,j que X soit égal à x_i et Y à y_j., est donc égale au rapport ci-dessous :

P(X = x_i, Y = y_j) = n_i,j/n = p_i,j

Exemple numérique : nous étudions le tableau ci-dessous, de taille suffisamment faible pour que les calculs puissent être effectués à l’aide d’une simple calculatrice.

Il rassemble les réponses d’une population de 200 étudiants aux questions X (sexe) et Y (couleur des cheveux). La question X comporte deux modalités (M et F, notées 1 et 2), la question Y trois modalités (blond, brun, autre, notées 1, 2, 3).

	Cheveux blonds (j = 1)	Cheveux bruns (j = 2)	Autre couleur (j = 3)	Effectifs marginaux
Masculin ( i = 1)	25	51	17	93
Féminin ( i = 2)	62	31	14	107
Effectifs marginaux	87	82	31	200

Tableau de contingence Sexe x Couleur de cheveux

(200 étudiants)

Formalisons l’exemple numérique précédent : ces effectifs n_i,j sont rassemblés dans le tableau de contingence ci-dessous.

					Question Y			marge
		y₁	y₂	...	y_j	...	y_q
	x₁	n_1,1	n_1,2	…	n_1,j	…	n_1,q	n₁.
	x₂	n_2,1	n_2,2		n_2,j		n_2,q	n₂.
	…	…	…		…		…	…
Question X	x_i	n_i,1	n_i,2	…	n_i,j	…	n_i,q	n_i.
	…	…	…		…		…	…
	x_p	n_p,1	n_p,2		n_p,j		n_p,q	n_p.
marge		n.₁	n.₂		n._j		n._q	n

Tableau 1.4 : Tableau de contingence (notations)

Les termes n₁., n₂., ... , n_i., ... donnent les effectifs des u.s. ayant répondu à la question X par les modalités x₁, x₂, ..., x_i, ....( n₁. = 93 étudiants de sexe masculin, n₂. = 107 de sexe féminin). La notation « i. » indique que c’est la ligne i qui est concernée.

Les termes n.₁, n.₂, ... , n._j, ... donnent les effectifs des u.s. ayant répondu à la question Y par les modalités y₁, y₂, ..., y_j, .....(n.₁ = 87 ont les cheveux blonds, n.₂ = 82 bruns, n.₃ = 31 d’une autre couleur). La notation « .j » indique que c’est la colonne j qui est concernée.

On distingue ainsi les termes de la ligne 1 notés 1. des termes de la colonne 1 notés .1 (idem pour 2., etc.). Ces effectifs n_i. et n._j sont appelés effectifs marginaux. Le nombre total de réponses étant noté n, on a évidemment :

	q			p
n_i. =	S	n_i,j	n._j =	S	n_i,j
	j = 1			i = 1

	p			q			p	q
n =	S	ⁿ_i.	=	S	ⁿ._j	=	S	S	n_i,j
	i = 1			j = 1			i = 1	j = 1

Du tableau de contingence on déduit un tableau contenant les proportions, en divisant simplement les effectifs par le nombre d’u.s.. Ce tableau de proportion est la loi de probabilité du couple de v.a. (X,Y) :

Définitions : (X, Y) étant un couple de v.a. qualitatives ou discrètes,

· on appelle loi de probabilité de ce couple l’ensemble des valeurs p_i,j définies par les rapports n_i,j/n :

p_i,j = P(X = x_i, Y = y_j) = n_i,j/n

· on appelle lois de probabilité marginales les lois de probabilité de X et Y définies par les suites de valeurs p_i. et p._j définies par les rapports n_i./n et n._j/n :

p_i. = P(X = i) = n_i./n

p._j = P(Y = j)= n._j/n

Exemple numérique : on déduit du tableau de contingence Sexe x couleur des cheveux le tableau de proportion ci-dessous, appelé aussi tableau de probabilité :

	Cheveux blonds (j = 1)	Cheveux bruns (j = 2)	Autre couleur (j = 3)	Marge en colonne
Masculin ( i = 1)	0.125	0.255	0.085	0.465
Féminin ( i = 2)	0.310	0.155	0.070	0.535
Marge en ligne	0.435	0.410	0.155	1

Tableau de probabilité et lois marginales

Remarque : les notations et définitions précédentes, données dans le cas d’un couple de v.a. qualitatives, sont les mêmes dans le cas d’un couple de v.a. discrètes. Le tableau des effectifs est alors équivalent à un tableau de corrélation.

5.2 Couples de variables aléatoires quantitatives.

Un couple de v.a. continues X et Y est une fonction qui, à chaque u.s. de la population W associe deux nombres réels x et y. Chaque variable X ou Y est appelée variable marginale et sa loi de probabilité, notée f_X(x) ou f_Y(y), loi de probabilité marginale.

Un exemple classique de couple de v.a. quantitatives est celui de la loi binormale. On se reportera au complément correspondant pour obtenir des précisions.

5.3 Indépendance de deux variables aléatoires.

Définition : on dit que deux variables X et Y sont indépendantes lorsque les événements « X Î I » et « YÎ J » sont indépendants quels que soient les sous-ensembles I et J.

Propriétés :

· Dans le cas de deux variables qualitatives ou discrètes indépendantes, le produit des densités marginales est égal à la densité du couple et chaque terme p_i,j est calculé par la formule ci-dessous :

p_i,j = p_i. p._j

· Dans le cas d’un couple gaussien, l’indépendance est équivalente à la nullité du coefficient de corrélation. Nous admettrons bien entendu cette propriété.

5.4 Lois conditionnelles.

La dernière classe de lois de probabilité que nous étudions est celle des lois conditionnelles. Nous nous limiterons aux v.a. discrètes ou qualitatives. Cette notion sera utilisée pour contrôler l’indépendance de deux variables qualitatives et en analyse factorielle des correspondances sous le nom de profil (chapitre 9).

Définition :

Soient X et Y deux variables discrètes ou qualitatives.

· on appelle loi de probabilité conditionnelle de Y sachant X = x_i la loi définie par la suite des probabilités conditionnelles P_Jⁱ = {p₁ⁱ, p₂ⁱ, p₃ⁱ, p₄ⁱ…, p_qⁱ) où :

p_jⁱ = P(Y = y_j / X = x_i)

· on appelle loi de probabilité conditionnelle de X sachant Y = j la loi définie par la suite des probabilités conditionnelles P_I^j = {p₁^j, p₂^j, p₃^j, p₄^j…,, p_p^j) où :

p_i^j = P(X = x_i / Y = y_j)

Propriété :

L’indépendance des variables X et Y est équivalente à l’égalité des lois conditionnelles en lignes (ou en colonnes).

La démonstration est assez facile et est donnée dans les compléments pédagogiques.

Exemple : à partir du tableau de contingence donnant la répartition des étudiants suivant leur sexe et la couleur des cheveux, on peut calculer deux sortes de répartitions appelées lois conditionnelles, exprimées souvent en pourcentages :

(i) la répartition des étudiants de sexe masculin suivant la couleur des cheveux, puis celles des étudiantes (lois conditionnelles en ligne) :

	Cheveux blonds	Cheveux bruns	Autre couleur	Total
Masculin	25/93 = 26.9%	51/93 = 54.8%	17/93 =18.3%	100%
Féminin	62/107= 57.9%	31/107= 29%	14/107= 13.1%	100%

Lois de probabilité conditionnelle en lignes

(ii) les répartition des étudiants blonds suivant leur sexe, puis des étudiants bruns et enfin des étudiants d'une autre couleur de cheveux (lois conditionnelles en colonne) :

	Cheveux blonds	Cheveux bruns	Autre couleur
Masculin ( i = 1)	25/87 = 28.7%	51/82 = 62.2%	17/31 = 54.8%
Féminin ( i = 2)	62/87 = 71.3%	31/82 = 37.8%	14/31 = 45.2%
Total	100%	100%	100%

Lois de probabilité conditionnelle en colonnes

· P_J¹ est la répartition des étudiants de sexe masculin suivant la couleur des cheveux.

· P_I² est la répartition des étudiants bruns suivant leur sexe.

L’indépendance consiste à dire que P_J¹ = P_J² (les garçons et les filles sont répartis de la même façon suivant la couleur des cheveux) ou que P_I¹ = P_I²= P_I³ ( les blonds, les bruns et les étudiants d’une autre couleur de cheveux sont répartis de la même façon suivant le sexe).

Conclusion

Nous nous sommes limités dans ce chapitre aux notions essentielles. La présentation, élémentaire, respecte les notions abstraites que l’on définit dans l’approche mathématique moderne. On notera que certaines notions nécessitent impérativement la maîtrise des fonctions exponentielle et logarithme, ainsi que le calcul intégral élémentaire, qui ne sont plus enseignés dans certaines sections de classes terminales françaises pourtant à vocation commerciale. Les étudiants issus de ces sections trouveront une introduction aux fonctions logarithme et exponentielle dans les compléments.

Table des matières

1. Probabilités. probabilités conditionnelles. 1

1.1 Population et événements. 1

1.2 Définition et propriétés des probabilités. 4

1.3 Indépendance et probabilité conditionnelle. 6

2. Variables aléatoires. lois de probabilité. 8

2.1 Variables aléatoires. 8

2.2 Probabilité d’un intervalle. 9

2.3 Loi de probabilité d’une v.a. discrète. 10

2.4 Loi de probabilité d’une v.a. continue. 12

2.5 Propriétés et calcul des probabilités. 14

3. Lois de probabilité discrètes. 15