Chapitre 3

régression et CORRéLATION

La corrélation est une notion couramment utilisée dans toutes les applications statistiques. Elle permet d’étudier la liaison que l’on rencontre fréquemment entre deux variables dans toutes les sciences humaines ou appliquées. Toutefois, la définition statistique de la corrélation est plus précise que le sens courant du terme : elle ne concerne que des variables statistiques quantitatives, c’est-à-dire dont on peut calculer les moyennes.

Considérons par exemple une étude menée par l’hypermarché EUROMARKET. Le directeur commercial de cet hypermarché se propose d’étudier l’âge et le revenu annuel de sa clientèle, afin de positionner l’hypermarché parmi la concurrence. Il commence bien entendu par analyser chaque critère séparément : calcul de l’âge moyen, du revenu moyen, etc.

Sa démarche consiste ensuite à détecter le lien entre les deux critères : comment ces deux critères sont-ils répartis dans la population observée l’un par rapport à l’autre ? Quelle est la nature de la liaison observée ? L’explication de cette liaison est-elle une information utile à la politique commerciale de l’entreprise ?

Dans le texte qui suit, les deux variables considérées jouent exactement le même rôle. La régression, fondée sur la notion de corrélation mais qui donne aux variables des rôles différents, est expliquée dans le chapitre 7.

1. Représentations graphiques.

Les données se présentent sous la forme d’une suite de n couples (x_i, y_i), numérotés de i = 1 à i = n. On note m_x, m_y, s_x², s_y², min_x, min_y et max_x, max_y, les moyennes, les variances et les valeurs minimales et maximales des séries (x_i) et (y_i).

La démarche initiale et indispensable pour étudier la liaison entre deux variables quantitatives consiste à représenter graphiquement les couples (x_i, y_i) observés.

1.1 Conventions élémentaires.

On utilise toujours un repère constitué de deux axes orthogonaux. Chaque axe correspond à une variable statistique (l’âge ou le revenu) et chaque point caractérise une unité statistique (un client).

Le calcul des valeurs extrêmes est indispensable pour choisir les échelles sur les axes. Si l’on veut construire le graphique à l’intérieur d’un espace défini par un rectangle de longueur L en abscisse et de largeur l en ordonnée, l’unité est égale à (max_x – min_x)/L sur l’axe des abscisses et à (max_y – min_y)/l sur l’axe des ordonnées.

Exemple : l’âge et le revenu des clients de l’hypermarché EUROMARKET ont les caractéristiques suivantes sur les données observées :

	Minimum	Maximum	Moyenne	Variance	écart-type
âge	24	68	40.06	87.2564	9.34111
revenu	72999	196484	107639.48	877095300.21	29615.79

Pour représenter les données (l’âge en abscisse, le revenu en ordonnée) dans un graphique à l’intérieur d’un rectangle de longueur L = 10 cm et de largeur l = 6 cm, on détermine les unités de longueur sur chaque axe :

u_x = (68 – 24)/10 = 4.4 : un centimètre représente 4.4 ans

u_y = (196484 – 72999)/6 = 20 580.83 : un centimètre représente 20 580.83 F

On peut naturellement simplifier les échelles, à condition toutefois de les diminuer pour que le graphique reste à l’intérieur du rectangle fixé. Par exemple :

u_x : 1 cm représente 5 ans

u_y : 1 cm représente 25 000F

On définit fréquemment comme origine des axes le point moyen (m_x, m_y) des observations. Le point i caractérisant l’unité statistique n°i a alors pour abscisse x_i – m_x et pour ordonnée y_i – m_y. On peut ainsi déterminer directement si l’unité statistique n°i définie par le couple (x_i, y_i) correspond à des valeurs supérieures ou inférieures aux moyennes m_x et m_y (cf. figure 1 ci-dessous).

Dans d’autres cas, on choisit une origine différente, définie par exemple par les valeurs observées les plus petites des séries (x_i) et (y_i), ou encore une origine qui a un sens précis dans le contexte des données. Le choix comme origine du point (0,0) n’a pas de signification particulière ; il peut simplifier la construction du schéma ou au contraire la compliquer en imposant des échelles aberrantes sur les axes (par exemple, l’origine (0,0) sur les données précédentes n’a aucun sens, l’âge minimum étant 24 ans et le revenu minimum 72999F).

L’origine du repère étant fixée au point moyen, les axes définissent quatre quadrants (on remarquera l’orthographe du mot quadrant) de la façon suivante :

Figure 1.3 : représentation graphique des couples (x_i, y_i)

En abscisse : x_i, en ordonnées : y_i

Origine des axes : moyennes m_x et m_y

La précision de la représentation n’étant pas primordiale, on peut se contenter souvent de papier ordinaire pour construire le schéma. En outre, il est préférable, suivant la place disponible et le nombre d’observations, de représenter les unités statistiques par leurs rangs, non par des points. Cela facilite leur identification.

Exemple : en figure 2, nous donnons la représentation graphique des couples (âge, revenu). L’origine des axes est le point moyen, et caractérise le couple (40.06, 107639.48) : tout point du côté positif de l’axe des abscisses caractérise un client plus âgé que la moyenne, tout point du côté négatif de l’axe des ordonnées caractérise un client dont le revenu est inférieur au revenu moyen, et inversement sur les deux axes.

Figure 2.3 : représentation graphique des couples (âge, revenu)

Origine des axes : moyennes de l’âge (40.06 ans) et du revenu (107639.48 F).

Le choix du client moyen comme origine des axes permet d’interpréter directement la position d’un client sur le graphique et la représentation des clients par leur rang permet leur identification immédiate. On constate un déséquilibre dans l’âge et le revenu des clients :

· beaucoup d’entre eux sont jeunes et disposent d’un revenu inférieur à la moyenne (quadrant III : n°37, 11, 6, 9, 18, 49, ...)

· les clients relativement âgés ont un revenu nettement supérieur aux autres (quadrant I : n°1, 10, 8) ;

· les personnes de soixante ans et plus (quadrant IV : n°25, 43, 31) disposent d’un revenu nettement inférieur à la moyenne. On peut penser qu’il s’agit de retraités.

Parmi les 50 personnes interrogées, celles qui sont relativement âgées reçoivent un revenu plus élevé que celles qui sont relativement jeunes. Les retraités sont nettement défavorisés.

Dans le cas de données nombreuses, la caractérisation des unités statistiques par leurs rangs est difficile. Un grand nombre d’entre elles risquent d’être absentes du schéma par manque de place, et il est alors préférable de caractériser les u.s. par des points. Le choix de l’origine des axes est soumis aux mêmes critères que précédemment.

1.2 Tableau de corrélation.

Une autre possibilité dans le cas de données nombreuses est de définir des intervalles sur chaque variable et de répartir les observations suivant ces intervalles. On obtient alors ce que l’on appelle le tableau de corrélation, dont le terme générique n_k,l est le nombre d’unités statistiques de la forme (x, y) telles que x appartienne à l’intervalle k défini sur la série (x_i) et y à l’intervalle l défini sur la série (y_i).

Cette procédure ne présente évidemment un intérêt que si les observations sont très nombreuses ou si on ne dispose pas des données individuelles.

Définition : on appelle tableau de corrélation des couples (x_i, y_i) i = 1, …, n le tableau d’effectifs obtenu par répartition des unités statistiques dans des intervalles fixés pour chaque série (x_i) i = 1, …, n et (y_i) i = 1, …, n.

Le calcul d’un tableau de corrélation est effectué à l’aide d’un algorithme analogue à ceux que nous avons donnés pour répartir des données dans des intervalles. L’algorithme le plus rapide consiste à chercher, pour chaque couple (x_i, y_i), dans quels intervalles I_k et J_l les valeurs x_i et y_i se trouvent et à augmenter de 1 le nombre d’observations appartenant à ces intervalles, puis à considérer le couple suivant. On obtient ainsi un tableau d’effectifs n_k,l. On construit ensuite la représentation graphique des couples (c_k, d_l) définis par les centres des intervalles à l’aide de disques dont l’aire est égale aux effectifs n_k,l.

Le calcul des aires est effectué de la façon suivante : on fixe l’aire du disque représentant l’effectif total à p l², l étant la largeur du rectangle dans lequel on veut construire la représentation graphique. L’aire du disque représentant n_k,l observations et dont on cherche le rayon r, est égale à p r² = p l² n_k,l / n. On en déduit :

r = l [n_k,l / n]^1/2

Exemple : nous avons réparti les observations dans les intervalles d’âge et de revenu suivants :

	Eff.	borne inférieure	supérieure	Moyenne	Centre
1	14	24	35	30.35714	29.5
2	27	35	46	39.85185	40.5
3	5	46	57	49.6	51.5
4	4	57	68	63.5	62.5

âge

	Eff.	borne inférieure	supérieure	Moyenne	Centre
1	26	72999	97696	87933.84	85347.5
2	14	97696	122393	108575.5	110044.5
3	5	122393	147090	135091.8	134741.5
4	2	147090	171787	158670.5	159438.5
5	3	171787	196484	194279	184135.5

revenu annuel

On répartit ensuite les couples d’observations pour obtenir le tableau de corrélation :

· Le client de rang 1 est âgé de 51 ans (intervalle 3) et gagne 195 888F (intervalle 5) : on le compte dans la cellule 3,5 ;

· Le client de rang 2 est âgé de 39 ans (intervalle 2) et gagne 128 456F (intervalle 3) : on le compte dans la cellule 2,3 ;

· Etc.

On obtient le tableau de corrélation suivant :

	l = 1	l = 2	l = 3	l = 4	l = 5
k = 1	13	1	0	0	0
k = 2	9	12	4	1	1
k = 3	1	1	1	1	1
k = 4	3	0	0	0	1

Tableau 1.3 : tableau de corrélation âge x revenu

(50 observations)

L’interprétation de la figure 3 ci-dessous, construite par ordinateur aboutit aux mêmes conclusions que précédemment. On ne peut toutefois caractériser les clients par leurs rangs pour obtenir d’autres informations.

Figure 3.3 : représentation graphique du tableau de corrélation.

On notera que le nombre de couples (50) est insuffisant pour que le calcul de ce tableau présente un intérêt autre que pédagogique.

1.3 Autres procédures.

Précisons pour finir d’autres procédures de représentations graphiques :

· Les axes orthonormés sont caractérisés par une même unité de longueur. Cela ne présente d’intérêt que si les variables sont exprimées dans la même unité ou si elles sont centrées réduites.

· Un axe peut être gradué suivant une échelle logarithmique : 1 cm représente par exemple un facteur 10 : Le premier centimètre représente 1 à 10, le second de 10 à 100, etc. En général, c’est l’axe des ordonnées qui est gradué de cette façon : il s’agit alors d’une échelle semi-logarithmique. Elle permet de représenter des valeurs dont la variation est très importante. Une propriété particulière classique de cette échelle semi-logarithmique est que la fonction exponentielle est représentée sous la forme d’une droite.

2. Coefficient de corrélation linéaire.

Le coefficient de corrélation linéaire de Bravais-Pearson, appelé souvent simplement coefficient de corrélation, est une mesure de la liaison entre les variables. Avant d’en préciser les propriétés et les limites, nous introduisons la notion de covariance en utilisant les propriétés illustrées dans la figure 1.

2.1 Covariance.

Comme nous l’avons expliqué précédemment, les deux variables sont liées quand une information sur l’une donne une information sur l’autre, plus précisément ici quand la position d’une des variables par rapport à la moyenne donne une indication sur la position de l’autre.

Les quatre quadrants définis par les axes contiennent des unités statistiques telles que :

dans le quadrant I :	x > mx, y > my	dans le quadrant II :	x < mx, y > my
dans le quadrant III :	x < mx, y < my	dans le quadrant IV :	x > mx, y < my

On en déduit le signe des produits (x – m_x) (y – m_y) dans chacun des quadrants :

quadrant I :	(x – mx) (y – my) > 0	quadrant II :	(x – mx) (y – my) < 0
quadrant III :	(x – mx) (y – my) > 0	quadrant IV :	(x – mx) (y – my) < 0

Supposons que la plupart des unités statistiques se trouvent dans les quadrants I et III. Les produits de la forme (x – m_x) (y – m_y) sont généralement positifs. Leur moyenne est positive et sera d’autant plus grande que les unités statistiques représentées dans les quadrants I et III seront nombreuses et éloignées de l’origine des axes.

Supposons que la plupart des unités statistiques se trouvent dans les quadrants II et IV. Les produits (x – m_x) (y – m_y) sont généralement négatifs, et par suite leur moyenne est négative. Cette moyenne sera d’autant plus petite (grande en valeur absolue) que les unités statistiques représentées dans les quadrants II et IV seront nombreuses et éloignées de l’origine des axes.

Lorsque la plupart des unités statistiques se trouvent régulièrement réparties dans les quatre quadrants, on ne constate pas de liaison entre les variables : les produits positifs et les produits négatifs se compensent plus ou moins les uns les autres. Leur moyenne est relativement proche de 0.

Exemple : les 50 clients de l’hypermarché se répartissent de la façon suivante dans les quatre quadrants :

quadrant I	(x > mx, y > my) :	12	quadrant II	(x < mx, y > my) :	6
quadrant III	(x < mx, y < my) :	25	quadrant IV	(x > mx, y < my) :	7

Les quadrants I et III contiennent 37 unités statistiques sur 50. L’âge et le revenu sont en général placés de façon identique par rapport à leurs moyennes : un client plus âgé que la moyenne (ou moins âgé) bénéficie en général d’un revenu supérieur à la moyenne (ou inférieur) et inversement. Les produits de la forme (x – m_x) (y – m_y) sont généralement positifs, et par suite leur moyenne.

Définition : on appelle covariance cov(x,y) de la série (x_i, y_i) la moyenne des produits de la forme (x_i – m_x) (y_i – m_y) :

	1	n
cov(x,y) =	–––	S	( xi – mx)( yi – my )
	n	i = 1

Le calcul de la covariance par la formule ci-dessus n’est guère commode : il faut d’abord calculer les moyennes, puis les différences, puis leur produit et enfin la moyenne des produits. On préfère utiliser une autre formule pour le calcul.

Propriété : la covariance est égale à la moyenne des produits moins le produit des moyennes.

	1	n
cov(x,y) =	–––	S	xi yi – mx my
	n	i = 1

Remarque : la covariance d’une variable avec elle-même est égale à la variance de cette variable : cov(x,x) = s_x².

2.2 Coefficient de corrélation linéaire.

La covariance est un paramètre statistique difficile à interpréter : comment évaluer la taille de ce paramètre ? A partir de quelle valeur peut-il être considéré comme « grand », ou « petit » ? Comment comparer deux covariances calculées sur des données totalement différentes ? La difficulté de répondre à ces questions est due en particulier au fait que la covariance dépend des unités de mesure choisies pour observer les séries (x_i) et (y_i).

Si l’âge est en années et le revenu en francs, la covariance entre l’âge et le revenu est en « années francs » ; si l’âge est en mois (1 année = 12 mois) et le revenu en dollars (1 F = 1/6 $), la valeur numérique de la « même » covariance sera égale à la précédente multipliée par 12 x 1/6 = 2. C’est pourquoi l’on préfère en général calculer la covariance des séries centrées réduites (x_i’) et (y_i’), qui sont indépendantes des unités de mesure, et dont les formules ont été données dans le chapitre 2 :

	xi – mx		yi – my
xi’ =	––––––	yi’ =	––––––––
	sx		sy

Définition : on appelle coefficient de corrélation linéaire de la série (x_i, y_i) la covariance des variable centrées réduites (x_i’, y_i’).

Formule : le coefficient de corrélation linéaire est égal à :

r(x,y) = cov(x,y)/s_x s_y

Le coefficient de corrélation est du même signe que la covariance et indépendant des unités de mesures. Nous verrons qu’il est compris entre –1 et 1. On peut donc comparer deux coefficients de corrélation calculés sur des données statistiques différentes.

Exemple de calcul : nous considérons ci-dessous une série de 10 couples d’observations. Nous en construisons la représentation graphique, puis calculons en détail le coefficient de corrélation.

i	xi	yi	i	xi	yi
1	-1.1281	-0.8054	6	0.8253	0.1334
2	1.0119	-0.4356	7	0.9883	-0.9250
3	-0.7513	0.4391	8	0.4276	0.0813
4	-0.3582	0.6185	9	-0.4186	-0.9395
5	-2.4488	0.7595	10	0.1263	-1.0540

Figure 4.3 : représentation graphique des dix couples (x_i, y_i)

Pour calculer le coefficient de corrélation linéaire entre les deux variables, on peut construire le tableau de calcul suivant :

i	xi	yi	xi²	yi²	xiyi	(xi-mx)²	(yi-my)²	(xi – mx)x (yi – my)
1	-1.1281	-0.8054	1.2727	0.6487	0.9086	0.9131	0.3512	0.5663
2	1.0119	-0.4356	1.0238	0.1898	-0.4408	1.4029	0.0497	-0.2639
3	-0.7513	0.4391	0.5644	0.1928	-0.3299	0.3349	0.4249	-0.3773
4	-0.3582	0.6185	0.1283	0.3826	-0.2215	0.0345	0.6910	-0.1543
5	-2.4488	0.7595	5.9966	0.5768	-1.8599	5.1813	0.9453	-2.2131
6	0.8253	0.1334	0.6811	0.0178	0.1101	0.9957	0.1198	0.3454
7	0.9883	-0.9250	0.9767	0.8557	-0.9142	1.3476	0.5073	-0.8268
8	0.4276	0.0813	0.1828	0.0066	0.0347	0.3602	0.0865	0.1765
9	-0.4186	-0.9395	0.1752	0.8826	0.3933	0.0605	0.5281	0.1788
10	0.1263	-1.0540	0.0160	1.1108	-0.1331	0.0893	0.7077	-0.2514

Ce tableau permet de calculer les moyennes, les variances, la covariance et le coefficient de corrélation linéaire. Les trois dernières colonnes, qu’on ne peut remplir qu’après le calcul de la moyenne, ne sont pas indispensables si on utilise les formules de calcul des variances et de la covariance. Elles permettent de détecter les unités statistiques particulières dans la liaison, ici l’unité statistique 5 dont on examinera la position sur la figure 4.

Cette unité statistique particulière donne un produit de la forme (x – m_x) x (y-m_y ) relativement élevé en valeur absolue par rapport aux autres. La covariance et par suite le coefficient de corrélation en dépendent beaucoup. On trouve :

	Sommes	Moyennes
des observations x	-1.7256	-0.1726
des observations y	-2.1277	-0.2128
des carrés x²	11.0178	1.1018
des carrés y²	4.8642	0.4864
des produits xy	-2.4527	-0.2453
des produits (x – mx)(y – my)	-2.8198	-0.2820
	variances	écarts-types
des observations x	1.0720	1.0354
des observations y	0.4411	0.6642

On en déduit le coefficient de corrélation :

r(x,y) =-0.2820 / (1.0354 x 0.6642)

Soit :

r(x,y) = -0.4101

Le coefficient de corrélation calculé sans tenir compte de l’u.s. 5 est égal à -0.0883 : son influence est donc très forte, comme on peut le supposer en examinant la figure 4.

Définitions :

· On appelle point aberrant dans la liaison entre deux variables statistiques un point qui est en contradiction flagrante avec la liaison constatée sur les autres observations.

· On appelle point influent dans la liaison entre deux variables statistiques un point qui accentue considérablement la liaison constatée sur les autres observations.

La recherche des points aberrants et influents est fondée sur la première règle de classification que nous avons donnée dans le chapitre 2.

Exemple : la représentation graphique donnée en figure 4 permet de détecter deux points particuliers :

· L’u.s. i = 1 est en contradiction avec la liaison observée sur les autres points, mais n’est pas suffisamment écartée du point moyen pour que l’on puisse la considérer comme aberrante.

· L’u.s. i = 5 à l’extrémité du nuage de points est une observation influente : la valeur x₅ est très petite par rapport à la moyenne et la valeur y₅ grande (cf. tableau de calcul). Elle accentue considérablement la liaison entre les variables.

Lorsque les données sont présentées sous la forme de données groupées (n_k, x_k, y_k), il suffit d’introduire les effectifs n_k dans les calculs des moyennes, variances et covariances.

Dans le cas d’un tableau de corrélation, à chaque couple (c_k, d_l) défini par les centres des intervalles k et l est associé l’effectif n_k,l. Le nombre d’observations x_i dans l’intervalle de centre c_k est noté n_k., le nombre d’observations y_i dans l’intervalle de centre d_l est noté n._l. Les moyennes et variances des centres sont pondérées par les effectifs n_k. pour les centres c_k, n._l pour les centres d_l. De même chaque terme dans le calcul de la covariance est pondéré par n_k,l.

En notant p et q les nombres des intervalles définis sur les x_i et y_i, la covariance est donnée par la formule ci-dessous :

	1	p	q
cov (c,d) =	–––	å	å	nk,l (ck – mc) (dl – md)
	n	k = 1	l = 1

On la calcule comme la moyenne pondérée des produits moins le produit des moyennes pondérées :

	1	p	q
cov (c,d) =	–––	å	å	nk,l ck dl – md mc
	n	k = 1	l = 1

Dans la formule précédente, la somme ne concerne que les produits de la forme n_k,l c_k d_l et le facteur 1/n ne divise que cette somme.

Comme précédemment, le coefficient de corrélation est le rapport de la covariance aux produits des écarts-types :

r(c,d) = cov(c,d) / (s_c s_d )

Exemple : Considérons la répartition des 50 clients suivant l’âge et le revenu des clients d’Euromarket donnée précédemment. On calcule tout d’abord les paramètres de chaque série d’observations en tenant compte des effectifs de chaque classe. :

l	dl	n.l	n.l dl	n.l dl^2
1	85.35	26	2219.1	189400.18
2	110.04	14	1540.56	169523.22
3	134.74	5	673.7	90774.34
4	159.44	2	318.4	50765.70
5	184.14	3	552.42	101722.61
Somme		50	5304.18	602186.05

revenu annuel

k	ck	nk.	nk. ck	nk. ck^2
1	29.5	14	413.0	12183.50
2	40.5	27	1093.5	44286.75
3	51.5	5	257.5	13261.25
4	62.5	4	250.0	15625.00
Somme		50	2014.0	85356.50

âge

Pour simplifier les résultats, nous avons exprimé les revenus en milliers de francs et ne conservons que deux décimales. On déduit de ces deux tableaux de calcul les variances et les écarts-types à l’aide des formules correspondantes :

	âge	revenu
Moyenne	40.28	106.08
Variance	84.65	790.75
Écart-type	9.20	28.12

Il reste à calculer le coefficient de corrélation, donc d’abord la covariance, égale à la moyenne des produits moins le produit des moyennes. Pour chaque classe de centre c_k définie sur l’âge et chaque classe de centre d_l définie sur le revenu, on calcule le produit n_k,l c_k d_l . On remplit ainsi le tableau ci-dessous :

	d1 = 85.35	d2 = 110.04	d3 = 134.74	d4 = 159.44	d5 = 184.14
c1 = 29.5	13x29.5x85.35	1x29.5x110.04	0	0	0
c2 = 40.5	9x40.5x85.35	12x40.5x110.04	4x40.5x134.74	1x40.5x159.44	1x40.5x184.14
c3 = 51.5	1x51.5x85.35	1x51.5x110.04	1x51.5x134.74	1x51.5x159.44	1x51.5x184.14
c4 = 62.5	3x62.5 85.35	0	0	0	1x62.5x184.14
Sommes	84240.45	62392.68	28766.99	14668.48	28449.63

La somme totale est égale à 218 518.23, et la moyenne des produits à 4 370.36. On en déduit la covariance :

cov(âge, revenu) = 4370.36 – 40.28 x 106.08 = 97.46

D’où enfin le coefficient de corrélation :

r(âge, revenu)= 97.46 / [9.20 x 28.12]

r(âge, revenu)= 0.377

La répartition des données dans un tableau de corrélation n’a pas modifié sensiblement les moyennes ni les variances. Par contre le coefficient de corrélation est égal à 0.377. Il est ici supérieur au coefficient de corrélation calculé sur les données individuelles (0.298), mais ce n’est pas toujours le cas. Avec toutes les décimales, on obtient r = 0.375.

On pourra vérifier cette stabilité du coefficient de corrélation en changeant de classes, en les caractérisant par leurs moyennes. Les calculs peuvent être effectués par StatPC.

3. Propriétés du coefficient de corrélation.

3.1 Propriétés mathématiques du coefficient de corrélation linéaire.

Propriété fondamentale : le coefficient de corrélation linéaire d’une série de couples d’observations (x_i, y_i) i = 1, …, n est compris entre -1 et 1. S’il est égal à ±1, les couples (x_i, y_i) i = 1, …, n vérifient exactement une relation linéaire de la forme :

quel que soit i = 1, …, n

a xi + b yi + c = 0

où a et b sont deux nombres réels constants et les points qui les représentent sont strictement alignés.

En fait, le coefficient de corrélation linéaire possède des propriétés mathématiques fondamentales analogues à celles du cosinus d’un angle.

La propriété fondamentale précédente est connue sous le nom d’inégalité de Schwarz.

3.2 Interprétation du coefficient de corrélation. Liaison linéaire.

L’interprétation du coefficient de corrélation linéaire n’est pas aussi facile qu’on le croit généralement :

· Plus il est proche de 1 ou de ‑1, plus les points sont proches d’une droite. S’il est égal à ± 1, les points sont strictement alignés.

· pour préciser une valeur à partir de laquelle on peut considérer le coefficient comme proche de 1 ou de –1, on utilise une table statistique (paragraphe 3.3).

· on peut obtenir des coefficients de corrélation très proches de 1 (0.95) sur des données non linéaires (par exemple, des données de la forme y = e^x).

· on peut obtenir des coefficients de corrélation nuls sur des données liées par une relation non linéaire exacte (cf. l’exemple donné plus loin).

· une relation statistique, détectée par le coefficient de corrélation ou par un graphique, ne montre jamais de relation causale entre deux variables. La causalité ne peut être déduite que d’une analyse non statistique des données.

Nous donnons ci-dessous trois schémas caractéristiques des valeurs du coefficient de corrélation dans le cas d’une liaison linéaire.

Lorsque le coefficient de corrélation est proche de 1 (il est égal à 0.9 en figure 5.1), les observations dans les quadrants I et III sont beaucoup plus nombreuses dans les quadrants II et IV et presque alignées le long d’une droite appelée axe principal.

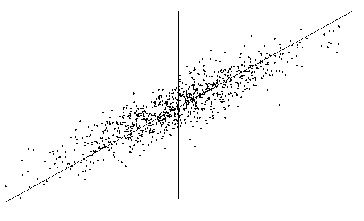
Figure 5.1.3 : Coefficient de corrélation proche de 1

En figure 5.2, le coefficient de corrélation est égal à –0.7: les observations sont plus nombreuses dans les quadrants II et IV et sont moins bien alignées. L’axe principal apparaît encore assez nettement.

Figure 5.2.3 : Coefficient de corrélation proche de –1

En figure 5.3, les observations sont réparties de façon uniforme dans les quatre quadrants : le coefficient de corrélation est très proche de 0 et l’axe principal n’apparaît plus.

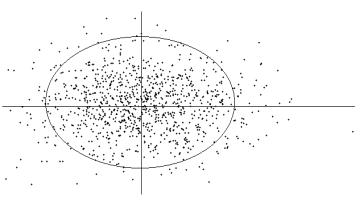
Figure 5.3.3 : Coefficient de corrélation proche de 0

L’axe principal représenté sur les graphiques n’est pas la droite de régression que nous définirons au chapitre 7. Il est déterminé de la façon suivante : c’est la droite telle que la somme des carrés des distances des points à cette droite soit la plus petite possible. Nous retrouverons cette notion dans le chapitre 9.

Exemple : le coefficient de corrélation entre l’âge et le revenu des 50 clients de l’hypermarché est égal à 0.298 sur les données individuelles. La figure 2 montre que les points sont relativement éloignés d’une droite du fait surtout des clients de rangs 25, 31 et 43. Le coefficient de corrélation n’est pas ici un paramètre statistique très fiable.

Une liaison dangereuse : nous donnons ci-dessous une série de 10 couples (x_i, y_i) tels que y_i soit égal à f(x_i) . Le lecteur pourra calculer le coefficient de corrélation r(x,y) et vérifier qu’il est égal à 0. La représentation graphique des couples montre une liaison fonctionnelle évidente qui n’est pas linéaire :

i	xi	yi	i	xi	yi
1	-0.5979	0.8868	6	-2.1125	-1.3455
2	1.5204	-0.1957	7	0.1706	1.0187
3	1.1423	0.3179	8	-1.9535	-0.9815
4	-0.0256	1.0451	9	0.6340	0.7997
5	2.4093	-1.8863	10	-1.1871	0.3409

10 couples liés fonctionnellement

dont le coefficient de corrélation est nul

Ce genre de liaison peut exister en particulier dans les analyses de séries chronologiques (chapitre 8) et multidimensionnelles (chapitre 9).

figure 6.3 : représentation d’un ensemble de couples

(x,y) tels que y= f(x), r(x,y) = 0

3.3 Répartitions normales.

Une autre condition pour que le coefficient de corrélation linéaire soit fiable est que les distributions des séries suivent à peu près la loi normale, c’est-à-dire que les histogrammes ne soient pas très différents de la courbe en cloche (cf. chapitre 1).

Lorsque cette propriété est vérifiée, on connaît la répartition du coefficient de corrélation calculé sur une série de n couples dont le coefficient de corrélation théorique est égal à 0. Nous anticipons ici sur le chapitre 6 pour donner une règle de classement de ce paramètre : un coefficient de corrélation supérieur en valeur absolue à la valeur donnée dans le tableau 2.3 pour le nombre d’observations correspondant montre l’existence d’une liaison réelle entre les variables.

n	valeur limite	n	valeur limite	n	valeur limite
10	0.6319	60	0.2542	150	0.1603
20	0.4438	70	0.2352	160	0.1552
30	0.3610	80	0.2199	170	0.1506
40	0.3120	90	0.2072	180	0.1463
50	0.2787	100	0.1966	200	0.1388

Tableau 2.3 : valeurs limites du coefficients de corrélation

Exemple : On donne ci-dessous l’histogramme des revenus des 50 clients observés d’Euromarket (figure ).

Figure 7.3 : Histogramme des revenus et courbe en cloche

(50 clients,5 intervalles de même amplitude)

Il est très différent de la courbe en cloche : les revenus ne sont pas répartis parmi les 50 clients d’Euromarket suivant la loi normale, et l’interprétation du coefficient de corrélation doit être prudente.

3.4. Matrices de corrélation.

L’analyse de la corrélation est beaucoup plus compliquée dans le cas de plus de deux variables. Dans l’exemple donné, on a observé simultanément l’âge, le revenu, le nombre d’enfants et les dépenses des 50 clients. Il y a donc 4 variables. Les coefficients de corrélation à calculer concernent :

· l’âge et successivement le revenu, le nombre d’enfants, les dépenses (3 coefficients) ;

· le revenu et successivement le nombre d’enfants, les dépenses (2 coefficients) ;

· le nombre d’enfants et les dépenses (1 coefficient).

Donc en tout 6 coefficients de corrélation.

Le même raisonnement nous montrerait que pour 10 variables, on a 45 coefficients de corrélation à calculer et que dans le cas général, pour p variables, le nombre de coefficients de corrélation est égal à p(p – 1) /2. Pour p = 20, cela donne 190 coefficients de corrélation.

Le problème n’est pas dans le calcul, vite résolu par le recours à l’informatique ; il est dans le tracé des graphiques, qui sont aussi nombreux que les coefficients de corrélation, et dans l’interprétation globale des relations entre les variables.

Il existe une méthode spécifique pour analyser ce genre de données : l’analyse en composantes principales, que nous expliquons rapidement dans le chapitre 9.

On présente en général les coefficients de corrélation sous la forme d’un tableau à double entrée, chaque ligne et chaque colonne du tableau correspondant à une variable. Un tel tableau est appelé matrice de corrélation et possède plusieurs propriétés, entre autres :

· La diagonale constituée des termes figurant à la i^e ligne et à la i^e colonne est constituée de 1 ;

· Il est symétrique par rapport à cette diagonale.

Exemple : nous donnons ci-dessous la matrice des corrélations entre l’âge, le revenu, les achats et le nombre d’enfants.

Le coefficient de corrélation entre l’âge et le nombre d’enfants est égal à –0.192. Il serait utile de représenter graphiquement les couples (âge, nombre d’enfants) pour expliquer pourquoi il est négatif. C’est là un des intérêts du coefficient de corrélation : il suscite des interrogations, auxquelles les réponses sont souvent intéressantes.

	âge	revenu	achats	nb. enfants
âge	1.000
revenu	0.298	1.000
achat	-0.132	0.137	1.000
nb. enfants	-0.192	0.384	0.626	1.000

4. Droite de régression.

Nous donnons une première approche de la régression linéaire, limitée à la statistique descriptive, que nous complétons dans le chapitre 7 dans le cadre général du modèle linéaire.

4.1 Critère des moindres carrés.

Figure 8.3 : Critère des moindres carrés

origine des axes en (m_x, m_y)

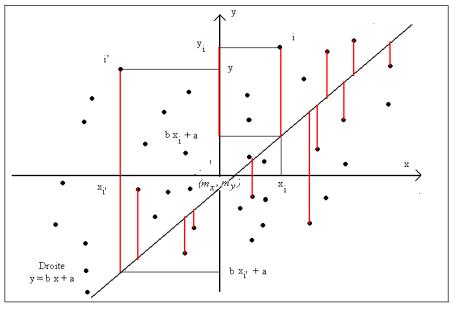
Nous avons représenté en figure 8.3 un ensemble de couples (x_i, y_i) i = 1, …, n en fixant l’origine du repère au point moyen (m_x, m_y). La droite que nous cherchons est la doite la plus proche possible des points, de façon que, pour chaque couple (x_i, y_i), l’ordonnée y_i soit la plus près possible de l’ordonnée b x_i +a du point de la droite d’abscisse x_i.

remarque : en mathématiques, l’équation d’une droite est notée y = a x + b. En statistique, l’usage est la notation choisie ici y = b x + a.

Critère des moindres carrés : Pour que chaque valeur y_i soit la plus proche possible de l’ordonnée b x_i + a du point d’abscisse x_i de la droite, on minimise la somme des carrés des différences :

	n
S =	S	[ yi – (b xi + a) ]^2
	i = 1

Les différences ïy_i – (b x_i + a)ï sont représentées sur la figure 8.3 par les longueurs des segments de couleur rouge (elles ne sont pas toutes représentées).

4.2 Estimation des coefficients de régression. Résidus.

Le calcul mathématique permet de déterminer les valeurs des coefficients b et a de façon que cette somme soit la plus petite possible.

Définition : on appelle droite de régression de Y en X calculée sur les couples (x_i, y_i)
i = 1, …, n la droite d’équation la plus proche des points de coordonnées (x_i, y_i) au sens des moindres carrés.

Remarque : on peut évidemment définir la droite de régression de X en Y. Cette procédure n’est pas compatible avec le modèle linéaire généralisée et il est préférable de ne pas en parler.

Théorème et définition : les coefficients b et a de la droite de régression sont appelés coefficients de régression. Ils sont donnés par les formules ci-dessous :

b = cov(x, y) / sx^2

= r sy / sx

a = my – b mx

Conséquence importante : la droite de régression toujours passe par le point moyen :

pour x = m_x, on obtient y = m_y.

Définition : on appelle résidu e_i le terme défini par la différence entre la valeur observée y_i et l’ordonnée du point de la droite de régression d’abscisse x_i, pour i = 1, …, n.

e_i = y_i – (b x_i + a) , i = 1, … n

Théorème : la série des résidus possède les propriétés suivantes :

· sa moyenne est nulle ;

· sa variance est égale à s² = (1 – r²) s_y², où r est le coefficient de corrélation des couples (x_i, y_i) i = 1, …, n, et s_y² la variance des y_i, i = 1, …, n ;

· le coefficient de corrélation entre les x_i et les e_i est égal à 0.

Les résidus e_i étant de moyenne nulle, leur variance est la moyenne de leurs carrés. Ils mesurent la proximité entre la droite et les points, et ce sont les plus petites erreurs possibles suivant ce critère. Plus la moyenne de leurs carrés est faible, plus la droite est proche des points.

Les propriétés des résidus s’expriment sous la forme ci-dessous :

1 - n

n S i = 1

ei = 0

1 - n

n S i = 1

ei^2 = (1 – r^2) sy^2

1 - n

n S i = 1

xi ei = 0

On suppose généralement que les résidus sont répartis à peu près suivant la courbe en cloche. La classification des résidus est alors donnée par la règle habituelle moyenne ± deux fois l’écart-type (cf.chapitre 2). La moyenne étant nulle, on comparera les résidus à l’écart-type et à deux fois l’écart-type.

4.3 Exemple : régression des revenus par l’âge des clients.

Nous avons analysé précédemment la relation existant entre le revenu et l’âge parmi les clients d’Euromarket. Nous abordons maintenant un problème différent : nous cherchons à reconstituer approximativement le revenu de quelqu’un en fonction de son âge. Il s’agit d’un problème de régression. Les résultats numériques ci-dessous sont obtenus par le logiciel :

équation de la droite de régression	y = 946.174 x âge + 69735.75
coefficient de corrélation linéaire	r = 0.298
variance des résidus	s^2 = 798 979 500

Figure 9.3 : représentation graphique des couples (âge, revenu)

Droite de régression et prévision du revenu pour 55 ans.

Les valeurs du revenu estimé pour 55 ans et 65 ans sont données par l’équation de la droite :

y = 946.174 x 55 + 69 735.75 = 121 775.3

y = 946.174 x 65 + 69 735.75 = 131 237.1

Ces estimations ne sont pas satisfaisantes :

· tous les clients âgés de 55 ans environ (n° 1, 8 et 10) ont un revenu largement supérieur à 121 775.32.

· tous les clients âgés de 65 ans environ (n° 25, 31 et 43) ont un revenu largement inférieur à la valeur estimée par la droite (131 237.1).

On peut le vérifier en effectuant le calcul des résidus : 

e1	=	195 888 – (946.174 x 51 + 69 735.75)	=	195 888 – 117 990	=	77 897.38
e8	=	155 989 – (946.174 x 53 + 69 735.75)	=	155 989 – 119 883	=	36 106.03
e10	=	196 484 – (946.174 x 57 + 69 735.75)	=	196 484 – 123 667.7	=	72 816.34

Le calcul des résidus e₂₅, e₃₁ et e₄₃ donne les résultats ci-dessous :

e25 = -51533.54

e31 = -47607.58

e43 = -60130.41

Suivant la régle, les résidus e₁, e₈ et e₁₀ peuvent être considérés comme grands (supérieurs à l‘écart-type 28 266.23) ou très grands (supérieurs à deux fois l’écart-type 56 532.45), tandis que les résidus e₂₅, e₃₁ et e₄₃ sont petits ou très petits. Le problème n’est pas l’existence de tels résidus, mais le fait que tous les résidus correspondant à l’âge de 55 ans soient grands et tous les résidus correspondant à l’âge de 60 ans petits.

L’analyse plus approfondie des résultats de la régression nécessite l’utilisation des probabilités et des tests statistiques. Nous en présentons les grandes lignes dans les chapitres suivants et revenons sur la régression linéaire dans le chapitre 7.

Conclusion.

Par son champ d’applications et les méthodes qui en découlent, l’analyse de la corrélation est une démarche fondamentale de la statistique appliquée.

La linéarité de la liaison et la forme en cloche des répartitions donnent au coefficient de corrélation des propriétés statistiques intéressantes, que nous développons dans les trois chapitres suivant. On se gardera bien d’expliquer la liaison entre deux variables par une relation de cause à effet, sans donner d’argument fort complétant l’approche statistique. Inversement, lorsque la taille du coefficient de corrélation est apportée comme argument démontrant la relation de causalité, il faut être conscient que ce raisonnement est très insuffisant (cf. exercice 4).

Table des matières

1. Représentations graphiques. 2

1.1 Conventions élémentaires. 2

1.2 Tableau de corrélation. 5

1.3 Autres procédures. 7

2. Coefficient de corrélation linéaire. 8

2.1 Covariance. 8

2.2 Coefficient de corrélation linéaire. 9

3. Propriétés du coefficient de corrélation. 15

3.1 Propriétés mathématiques du coefficient de corrélation linéaire. 15

3.2 Interprétation du coefficient de corrélation. Liaison linéaire. 16

3.3 Répartitions normales. 18

3.4. Matrices de corrélation. 20

4. Droite de régression. 21

4.1 Critère des moindres carrés. 21

4.2 Estimation des coefficients de régression. Résidus. 22

4.3 Exemple : régression des revenus par l’âge des clients. 23

Conclusion. 25