Chapitre 2

CARACTÉRISTIQUES numériques

Lorsque les données sont quantitatives, les représentations graphiques sont complétées par des valeurs numériques, appelées aussi caractéristiques, indiquant les propriétés des données. Les variables quantitatives discrètes (à valeurs entières), les données ordinales (qui sont des classements par ordre de préférence) et les échelles de notes peuvent être assimilées aux données quantitatives.

Exemple : dans le chapitre précédent, les informations obtenues auprès des clients ont été présentées graphiquement. Il s’agit maintenant de proposer des paramètres numériques donnant une indication sur le montant de leurs achats.

Pour comparer sa clientèle à celles des autres hypermarchés, le responsable commercial a besoin d’un ordre de grandeur du montant des achats. Les calculs sont effectués sur les 50 clients – l’échantillon observé – mais ce sont les propriétés concernant l’ensemble de la clientèle – la population de référence– qui sont intéressantes : nous verrons dans le chapitre 5 comment aborder ce problème. Les données figurent dans le tableau 2.2 du chapitre 1.

1. Caractéristiques de tendance centrale.

Dans le chapitre précédent nous avons défini la classe modale comme celle dont la densité est la plus grande. Les valeurs caractéristiques que nous introduisons dans ce chapitre sont fondées sur une notion différente, celle de distance : pour trouver l’ordre de grandeur des observations, nous cherchons une valeur la plus proche possible de la série d’observations.

1.1 Notion de distance.

La série de données se présente sous la forme d’une suite de nombres x_i numérotés
de i = 1 à i = n. Par exemple, le montant des achats du premier client est x₁ = 150.15, celui du 10^e est x₁₀ = 555.10. Pour évaluer la proximité entre ces deux achats, il est naturel d’en calculer la différence, et, cette proximité entre x₁ et x₁₀ étant la même qu’entre x₁₀ et x₁, on peut considérer la valeur absolue ou le carré de cette différence :

x1 – x10 = = – 404.95

ç x1 – x10 ç = 404.95

(x1 – x10)^2 = (– 404.95)^2

Comment évaluer maintenant la proximité entre une valeur x et les n observations x_i ? Deux méthodes (parmi d’autres) sont possibles :

· on considère la somme e_x des valeurs absolues des différences entre x et les x_i :

		n
ex = ï x – x1 ç + ç x – x2 ç + ç x – x3 ç + ...	=	å	ç x – xi ç
		i = 1

· on considère la somme d définie par son carré :

		n
dx^2 = [ x – x1 ]^2 + [ x – x2 ]^2 + [ x – x3 ]^2 + ...	=	å	[ x – xi ]^2
		i = 1

Chacun de ces deux paramètres e_x et d_x² caractérise la proximité entre la valeur x et la série des observations x_i : plus e_x ou d_x² est grand, plus x est différent des x_i. Ce sont en quelque sorte des « distances » entre la valeur x et la série (x_i) i= 1, …, n.

1.2 Caractéristiques de tendance centrale ; médiane, moyenne.

Pour déterminer l’ordre de grandeur des observations x_i, il suffit de calculer la valeur x qui en est la plus proche possible. Chaque distance précédente conduit à un paramètre :

· la somme des valeurs absolues des différences e_x est minimale lorsque x est une valeur appelée médiane qui possède la propriété caractéristique suivante :

la médiane est une valeur telle que la moitié des

observations x_i lui soient inférieures ou égales

La médiane est appelée aussi parfois moyenne. Elle n’existe pas dans certains cas et n’est pas toujours unique : on se contente alors d’une valeur approximative, comme dans l’exemple numérique ci-dessous. Nous noterons la médiane m_é.

· la somme des carrés des différences d_x² est minimale lorsque x est égale à la moyenne notée m des observations (c’est le critère des moindres carrés) :

	(x1 + x2 +x3 + x4 + ... )		1	n
m =	––––––––––––––––––	=	–––	å	xi
	n		n	i = 1

Exemple numérique : on donne ci-dessous une série de 6 observations :

x₁ = 10, x₂ = 11, x₃ = 12, x₄ = 13, x₅ = 14, x₆ = 15

La moyenne de ces 6 observations est égale à 12.5, et on choisit comme médiane la moyenne de x₃ et x₄ : 12.5 (3 observations sont inférieures à 12.5 et 3 sont supérieures).

Supposons que x₁ prenne la valeur 0. La moyenne devient 10.83, la médiane reste égale à 12.5.

Les propriétés de la médiane et de la moyenne sont les suivantes :

· la médiane a pour avantage d’être peu sensible aux valeurs numériques de la série ; elle ne dépend guère que de l’ordre des observations et est constante même si les premières et dernières observations varient considérablement. Elle n’est pas toujours facile à calculer, et parfois même n’existe pas.

· La moyenne possède des propriétés mathématiques intéressantes et est facile à manipuler mathématiquement. Elle dépend de toutes les valeurs x_i et particulièrement des valeurs x_i très grandes en valeur absolue, surtout si les observations sont peu nombreuses.

En conséquence,

· lorsque les données sont peu nombreuses, que certaines observations sont très élevées en valeur absolue, et qu’il existe un risque d’erreur de mesure non négligeable, on choisira la médiane comme ordre de grandeur des observations. Ainsi, dans le petit exemple numérique précédent, si l’on considère que x₁ ne peut pas raisonnablement être égale à 0, et qu’il y a donc erreur, on choisira la médiane.[1]

· lorsque les observations sont précises, fiables et relativement nombreuses, on choisira la moyenne comme ordre de grandeur des observations.

Exemple : La médiane et la moyenne des achats des 50 clients sont :

moyenne : m = 316.945

médiane : mé = 264.14

La médiane est ici la moyenne des 25^e et 26^e observations après classement dans l’ordre croissant :

x13 = x(25) = 254.13

x24 = x(26) = 274.15

Cas de données classées : il arrive que les données étudiées soient groupées par valeur ou aient été réparties dans des intervalles (cf. exercice 1 du chapitre 1) . S’il est en général difficile de calculer la médiane (on peut utiliser une interpolation linéaire, comme dans StatPC), on peut calculer la moyenne en supposant que dans chaque classe, les observations sont toutes égales au centre de cette classe. Pour calculer la moyenne appelée moyenne pondérée, on utilisera alors la formule ci-dessous dans laquelle :

· n est le nombre total d’observations ;

· p le nombre de classes ;

· n_k le nombre d’observations appartenant à la classe de centre c_k :

	n1 c1 + n2 c2 + ... + np cp		1	p
mc=	––––––––––––––––––––––––	=	–––	å	nk ck
	n		n	k = 1

Remarque : en caractérisant chaque classe par la moyenne des observations qui lui appartiennent, la moyenne pondérée est la moyenne des données individuelles (exercice 7).

2. Caractéristiques de dispersion.

La moyenne et la médiane donnent chacune un ordre de grandeur des observations : ce sont des caractéristiques de « tendance centrale ». Mais il est facile d’imaginer des séries d’observations ayant même moyenne et même médiane alors qu’elles sont très différentes.

Exemple numérique : on considère la série de 6 observations : x₁ = 10, x₂ = 11,
x₃ = 12, x₄ = 13, x₅ = 14, x₆ = 15. Nous avons vu que la moyenne et la médiane sont égales à 12.5. La série :x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 23, x₅ = 24, x₆ = 25 a la même moyenne et la même médiane que la première. Elle en est pourtant très différente : les observations sont beaucoup plus écartées les unes des autres.

2.1 Ecart absolu moyen, variance et écart-type.

Pour compléter la caractéristique de tendance centrale par un paramètre évaluant la « dispersion » des observations, on évalue la distance entre cette caractéristique et la série des observations x_i :

· on considère la somme e_x des valeurs absolues des différences entre la médiane m_é et les x_i :

		n
emé = ï x1 – mé ç + ç x2 – mé ç + ç x3 – mé ç + ...	=	å	ç xi – mé ç
		i = 1

· on considère la somme des carrés des différences entre la moyenne m et les x_i :

		n
dx^2 = [ x1 – m ]^2 + [ x2 – m ]^2 + [ x3 – m ]^2 + ...	=	å	[ xi – m ]^2
		i = 1

Dans la pratique, on recherche des ordres de grandeur des écarts çx_i – m_é ç ou des carrés (x_i – m)². Ces ordres de grandeur sont donnés par les moyennes (même s’il serait plus logique de considérer la médiane des écarts ç x_i – m_é ç dans le premier cas). On définit ainsi :

· l’écart absolu moyen e_am , m_é étant la médiane :

	1	n
eam =	–––	å	ç xi – mé ç
	n	i = 1

· la variance s² , m étant la moyenne :

	1	n
s^2 =	––––	å	[ xi – m ]^2
	n	i = 1

· la racine carrée s de la variance s² est appelée écart-type : elle s’exprime dans la même unité que les observations.

Il n’y a pas de procédure simple pour calculer l’écart absolu moyen. Par contre, pour calculer la variance, on dispose de la formule ci-dessous :

	1		1	n
s^2 =	–––	( x1^2 + x2^2 + x3^2 + ... ) – m^2 =	–––	å	xi ^2 – m^2
	n		n	i = 1

Dans cette formule, s² apparaît comme la moyenne des carrés moins le carré de la moyenne. C’est cette formule qu’il faut employer pour effectuer le calcul d’une variance.

Remarque : on définit aussi la variance de façon légèrement différente en divisant par ( n – 1 ) au lieu de n dans la formule précédente. Nous en donnons l’explication dans le chapitre 5. Nous utilisons toujours la première définition qui permet d’effectuer les calculs plus simplement.

Exemple numérique : on considère la série de 6 observations : x₁ = 10, x₂ = 11,
x₃ = 12, x₄ = 13, x₅ = 14, x₆ = 15. Nous avons vu que la moyenne est égale à 12.5. Nous admettons que l’écart absolu moyen est égal à 1.5. La somme des carrés est égale à 955. On en déduit la variance, égale à la moyenne des carrés moins le carré de la moyenne :

s^2 = ( x1^2 + x2^2 + x3^2 + ... ) /n – m^2

= 955/6 – 12.5^2 = 159.167 – 156.25

On en déduit :

s^2 = 2.917

s = 1.708.

eam = 1.5

On sait que la série suivante : x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 23, x₅ = 24, x₆ = 25, a la même moyenne et la même médiane que la précédente. Elle en est pourtant très différente : l’écart-type (11.53) et l’écart absolu moyen (11.5) sont beaucoup plus grands que les précédents.

Cas de données classées : on procède comme pour calculer la moyenne en supposant que les observations de chaque classe sont égales au centre de la classe. On applique alors la formule ci-dessous avec les mêmes notations que dans le paragraphe précédent :

s_c² = [n₁ c₁² + n₂ c₂² + ... + n_p c_p²] / n – m_c²

Soit :

	1	p
sc^2 =	–––	å	nk ck^2 – mc^2
	n	k = 1

Exemple : on donne ci-dessous la variance, l’écart-type et l’écart absolu moyen des achats des 50 clients :

s^2 = 42902.472

s = 207.129

eam = 150.8346

C’est l’écart-type, qui est le plus utilisé dans la pratique, en particulier pour comparer deux valeurs entre elles ou une valeur et la moyenne.

Il possède en effet une propriété qui facilite son interprétation : c’est une moyenne particulière (appelée moyenne géométrique) des écarts entre les observations et leur moyenne. L’écart absolu moyen et l’écart-type donnent deux ordres de grandeur des écarts de la forme ½x_i – m_x½. Ils sont exprimés dans la même unité que les observations.

2.2 Comparaison d’une valeur à la moyenne.

L’important est de bien comprendre qu’il n’est pas possible de comparer une valeur à la moyenne ou deux valeurs entre elles sans tenir compte de l’écart-type.

Nous proposons dans le tableau 1.2 une première règle de classification et une terminologie que l’on adaptera suivant la nature des données analysées :

différence x – m	valeur centrée réduite	caractérisation	pourcentages
x – m < – 2 s < 0	(x – m)/s < – 2	x est très petite ;	2.5%
– 2 s < x – m < – s	– 2 < (x – m)/s < – 1	x est petite ;	12.5%
– s < x – m < s	– 1 < (x – m)/s < 1	x est ordinaire;	70 %
2 s > x – m > s	2 > (x – m)/s > 1	x est grande ;	12.5%
x – m > 2 s >0	(x – m)/s > 2	x est très grande ;	2.5%

Tableau 1.2 : première règle de classification des valeurs

Cette règle est justifiée lorsque l’histogramme est proche de la courbe en cloche dont nous avons parlé dans le chapitre 1 : les pourcentages obtenus doivent être d’autant plus voisins des pourcentages indiqués ci-dessous que le nombre d’observations est important. Si l’histogramme est différent de la courbe en cloche, ces pourcentages peuvent être très différents, et la règle proposée présente moins d’intérêt.

Exemple : appliquons la règle précédente aux achats des 50 clients :

m – 2 s	= – 97.3132	m – s	=	109.8159
m + s	= 524.0741	m + 2 s	=	731.2032

Il n’y a pas de très petites valeurs. C’est dû à l’asymétrie de la répartition que l’on peut constater en examinant un des histogrammes donnés dans le chapitre précédent.

Petites valeurs inférieures à 109.8159	: x5, x28, x4, x3, x29, x30, x31
Grandes valeurs supérieures à 524.0741	: x10, x37, x39, x11, x12
Très grandes valeurs supérieures à 731.2032	: x8, x9, x27

2.3 Valeurs centrées réduites

Les deux premières colonnes du tableau 1.2 contiennent des relations équivalentes. La deuxième contient les valeurs centrées réduites, dont l’utilisation est très fréquente en statistique.

Définition : on appelle observations centrées réduites de la série (x_i) les observations de la forme x_i’ = (x_i – m)/s, expression dans laquelle m et s sont respectivement la moyenne et l’écart-type des observations x_i .

	xi – m
xi^’ =	–––––––––
	s

· Les valeurs x_i’ sont dites centrées parce que leur moyenne m’ est nulle.

· Elles sont dites réduites parce que leur variance est égale à 1.

L’intérêt des valeurs centrées réduites est dû en particulier au fait qu’elles sont indépendantes des unités de mesure utilisées pour effectuer les observations.

Exemple : on a, suivant que les achats sont exprimés en francs ou en euros (1 euro = 6.5 F) :

	x26	Moyenne	Écart-type	calcul	x26’
en francs	314.25	316.945	207.129	(314.25 – 316.945)/207.129	= – 0.013
En euros	48.33	48.761	31.866	(48.35 – 48.76 )/31.866	= – 0.013

3. Autres paramètres.

3.1 Coefficient de variation

Un autre paramètre, important en marketing, est le coefficient de variation : il indique en pourcentage l’ordre de grandeur des variations des observations autour de la moyenne. Il n’a de sens que si les données sont positives.

Définition : Le coefficient de variation est le rapport de l’écart-type à la moyenne exprimé en pourcentage :

c_v = (s/m ) x 100%

L’interprétation du coefficient de variation repose sur la propriété suivante : pour une répartition régulière et à peu près symétrique, on peut dire qu’il y a à peu près 70% des observations égales à la moyenne ± c_v%.

En fait, on retrouve ici l’intervalle m ± s que nous avons indiqué dans la première règle de classification.

Exemple : la moyenne des achats des clients est égale à 316.945F et l’écart-type à 207.129. Le coefficient de variation est donc : c_v= 65.35%

Les achats sont de l’ordre de 317F ± 65% sous réserve que l’histogramme soit relativement symétrique. Par le calcul on trouve effectivement 70% des achats compris entre la moyenne ± l‘écart-type bien que l’histogramme donné en figure 12 du chapitre 1 ne ressemble guère à la densité de la loi normale.

3.2 Coefficients de forme

On définit d’autres coefficients pour caractériser la forme de l’histogramme.

Définition : Le coefficient d’asymétrie est la moyenne des cubes des valeurs centrées réduites des observations.

	1	n
cas =	–––	S	[ (xi – m)/s ]^3
	n	i = 1

étudions les termes [ (x_i – m)/s ]³ en nous référant à la règle (on note >> pour très supérieur et << pour très inférieur) :

xi’ = (xi – m)/s > 1	xi grand ou très grand	[ (xi – m)/s ]^3 >>1
xi’ = (xi – m)/s< – 1	xi petit ou très petit	[ (xi – m)/s ]^3 <<– 1
– 1< xi’ = (xi – m)/s <1	xi relativement proche de m	[ (xi – m)/s ]^3 @ 0

Ce sont les termes « grands » ou « petits » qui interviennent le plus dans le calcul du coefficient d’asymétrie, puisqu’ils sont supérieurs à 1 en valeur absolue et que leurs cubes le sont d’autant plus (par exemple 1.5³ = 3.375) ; les autres, inférieurs à 1 en valeur absolue, positifs ou négatifs, ont un cube plus petit en valeur absolue (par exemple 0.8³ = 0.512) et n’ont guère d’influence sur la somme.

Lorsque les observations grandes ou très grandes sont à peu près aussi nombreuses que les observations petites ou très petites, ou qu’il y en a peu, le coefficient d’asymétrie est proche de 0 ;

· lorsque les observations grandes ou très grandes sont plus nombreuses que les observations petites ou très petites, le coefficient d’asymétrie est supérieur à 0 ;

· lorsque les observations grandes ou très grandes sont moins nombreuses que les observations petites ou très petites, le coefficient d’asymétrie est inférieur à 0 ;

La valeur à partir de laquelle on peut considérer le coefficient d’asymétrie comme très différent de 0 dépend du nombre d’observations. Elle est donnée dans une table statistique figurant dans StatPC (pour n = 50, on pourra considérer que le coefficient d’asymétrie est très différent de 0 s’il est supérieur en valeur absolue à 0.534). Nous donnons un extrait de cette table dans le tableau 2 .2.

Définition : le coefficient d’aplatissement est la moyenne des puissances quatrièmes des observations centrées réduites :

	1	n
cap =	–––	S	[ (xi – m)/s ]^4
	n	i = 1

Ce coefficient caractérise « l’aplatissement » de l’histogramme par rapport à « l’aplatissement » de la densité de loi normale dont le coefficient théorique est égal à 3. On l’interprète de façon analogue au coefficient d’asymétrie, en examinant la fréquence des termes très grands et très petits.

· Si l’histogramme est proche de la densité de la loi normale, le calcul mathématique montre que le coefficient d’aplatissement est proche de 3 ;

· Si les termes différents de la moyenne sont plus nombreux que dans le cas de la loi normale, les termes de la forme [(x_i – m )/ s]⁴ supérieurs à 1 sont plus nombreux et le coefficient d’aplatissement est supérieur à 3, et inversement.

Ce coefficient n’est guère interprétable que si la répartition est à peu près symétrique (a_s @ 0). Il caractérise ce que l’on appelle les « queues de distribution » (les termes très petits ou très grands), au-dessus de la courbe en cloche (c_ap > 3) ou en dessous (c_ap < 3).

Un coefficient d’aplatissement inférieur à 2.15 ou supérieur à 3.99 peut être considéré comme différent de 3 lorsque le nombre d’observations est égal à 50 (cf. tableau 2.2). Il existe une table statistique donnant les autres valeurs limites (elle figure dans StatPC).

En pratique , ces coefficients servent à contrôler la proximité de l’histogramme et de la courbe en cloche :

· c_as @ 0 et c_ap @ 3 : la répartition des données est plus ou moins normale ;

· c_as ¹ 0 ou c_ap ¹ 3 : la répartition des données est différente de la loi normale.

Cette démarche, assez approximative ici, sera formulée en terme de test statistique dans le chapitre 7.

nombre d’observations	coefficient d’asymétrie	coefficient	d’aplatissement
10	0.954	1.560	3.950
20	0.772	1.820	4.170
30	0.662	1.980	4.110
40	0.587	2.070	4.060
50	0.534	2.150	3.990

Tableau 2.2 : valeurs limites des coefficients d’aplatissement et d’asymétrie

Exemple : le coefficients d’aplatissement sur les achats des 50 clients est c_ap = 3.859. On ne peut pas affirmer que l’aplatissement est différent de celui de la courbe en cloche. La taille élevée du coefficient d’asymétrie (c_as = 1.16) rend difficile son interprétation et suffit pour montrer que la répartition des achats est très différente de la courbe en cloche.

4. Fonction de répartition. quantiles.

L’introduction de la fonction de répartition va nous être utile pour définir les quantiles dont l’utilisation dans les statistiques officielles est très fréquente, ainsi que la notion de concentration bien connue en gestion sous le nom de règle des 80%– 20%.

4.1 Fonction de répartition

Définition : on appelle fonction de répartition d’une série d’observations (x_i) i = 1, …n la fonction qui, à un nombre réel quelconque x , associe la proportion d’observations inférieures ou égales à x. On la note en abrégé f.d.r.

Exemple numérique : on considère la série de 6 observations : x₁ = 10, x₂ = 11.5, x₃ = 12, x₄ = 13, x₅ = 14.5, x₆ = 15 . La fonction de répartition précédente est constante et égale à 1/6 sur chaque intervalle séparant deux observations successives, par exemple sur l’intervalle [11, 12 [.

Figure 1.2 : Fonction de répartition (6 observations)

La fonction de répartition, notée en général par F(x), est définie pour tout nombre x. Elle possède des propriétés évidentes que l’on constate sur la figure 2 :

· En notant inf(x_i) et sup(x_i) la plus petite et la plus grande des valeurs observées, on a :

Pour tout x < inf (xi)

F(x) = 0

Pour tout x ³ sup(xi)

F(x) = 1

En effet , le nombre d’observations strictement inférieures à la plus petite d’entre elles est nul, et le nombre d’observations inférieures ou égales à la plus grande est égal à n.

· Elle est croissante : x £ x’Þ F(x) £ F(x’). Cela correspond à la propriété suivante (figure 1) : le nombre d’observations inférieures à x = 10 est plus petit que le nombre d’observations inférieures à x’ =12. Cette propriété est vraie dès que x £ x’.

· C’est une fonction « en escalier », c’est– à– dire qu’elle est constante sur des intervalles successifs. .

Il est commode de classer les observations par valeurs croissantes : x(1), x(2), ..., x(n). La valeur x(1) est la plus petite valeur observée, et x(n) la plus grande. Soient x(i) et x(i+1) les observations de rang i et i+1 ( on suppose x(i) < x(i+1) ). Le nombre d’observations inférieures ou égales à x est constant et égal à i quel que soit x appartenant à l’intervalle [x(i), x(i+1) [.

On a ainsi :

quel que soit x Î [x(i), x(i+1) [

F(x) = i/n

Dans l’intervalle suivant [x(i+1), x(i+2) [ , on a :

quel que soit x Î [x(i+1), x(i+2) [

F(x) = ( i + 1 )/n

La fonction augmente donc par palier de 1/n. Dans le cas où deux observations sont égales : x(i) = x(i+1), la fonction augmente de 2/n. Dans le cas général, elle augmente d’un multiple de 1/n et reste constante sur chaque intervalle.

La fonction de répartition exacte d’une série d’observations n’est pas difficile à calculer, mais c’est un travail long et fastidieux. On se limite souvent à en calculer la valeur en quelques points, que l’on joint entre eux par un segment de droite (c’est une interpolation linéaire) ou inversement on détermine les points auxquels elle prend une valeur fixée.

Exemple : nous avons calculé par ordinateur la fonction de répartition des achats des 50 clients d’EUROMARKET. Il s’agit ici d’un calcul exact.

Figure 2.2 : Fonction de répartition des achats

On constate que la proportion d’achats augmentent assez vite pour les petits montants, et plus lentement à partir d’environ 215F.

4.2 Quantiles, quartiles, déciles ...

Plutôt que d’étudier la fonction de répartition elle– même, on préfère souvent en déduire les « quantiles » , qui caractérisent la répartition des n observations en classes de même effectif.

On n’utilise les quantiles que lorsque le nombre d’observations est suffisant. On peut considérer que les classes doivent avoir un effectif d’au moins 5 observations, d’où les conditions d’effectifs proposées ci-dessous :

la médiane	mé	deux classes d’effectifs n/2	(50%)	n³10
les quartiles	q1, q2 = mé, q3	quatre classes d’effectifs n/4	(25%)	n³20
les quintiles	r1, r2, r3, r4, r5	cinq classes d’effectifs n/5	(20%)	n³25
Les déciles	d1, d2, ..., d9	dix classes d’effectifs n/10	(10%)	n³50
Les centiles	c1, c2, ..., c99	cent classes d’effectifs n/100	(1%)	n³500

Ces paramètres présentent les mêmes inconvénients de calcul que la médiane : il n’est pas toujours facile de les déterminer. Par exemple, les quartiles d’une série de 50 observations n’existent pas. On considère alors des approximations :

· Le premier quartile est défini par toute valeur comprise entre la 12^e et de la 13^e observation ;

· le deuxième quartile (la médiane) est défini par toute valeur comprise entre la 25^e et de la 26^e observation ;

· le troisième quartile est défini par toute valeur comprise entre la 47^e et de la 48^e observation .

En général (mais une interpolation linéaire est possible), on considère les moyennes des observations précédentes pour donner une valeur précise aux quartiles.

Les millimes, les dix-millimes, les cent-millimes, qui correspondent aux fractions 1/1000, 1/10 000, 1/100 000 de l’effectif total, sont utilisés par l’INSEE pour caractériser les séries d’observations très nombreuses.

Une première application des quantiles est la vérification de la symétrie de la répartition. Dans la pratique, on considérera que la répartition est symétrique si :

· La médiane et la moyenne sont à peu près égales ;

· La médiane est à peu près la moyenne des quartiles q₁ et q₃, des déciles d₁ et d₉, d₂ et d₈, etc…

Une seconde application des quantiles est le calcul du rapport entre la plus petite et la plus grande des valeurs d’une série d’observations. Dans la mesure où ces observations sont tirées au hasard, ce rapport peut varier considérablement d’un tirage à l’autre et son instabilité le rend discutable. On préfère calculer le rapport du dernier dix-millime ou cent-millime au premier. C’est ce que fait l’INSEE en étudiant les revenus ou les patrimoine des Français.

Exemple : Pour calculer les quantiles des achats des 50 clients, on classe les observations suivant les valeurs croissantes (tableau 6.1 du chapitre 1).

On définit les déciles comme les moyennes des observations de rang 5 et 6, de rangs 10 et 11, 15 et 16 etc.… Nous les avons représentés en figure 3. On obtient :

d1 = 97.560	d2 =152.405	d3 = 190.665	d4 = 241.340	d5 = 264.140
d6 = 300.575	d7 = 335.670	d8 = 484.715	d9 = 621.515	d10 = 951.160

Nous pouvons maintenant introduire une autre règle pour évaluer la taille d’une observation.

f.d.r.	caractérisation	Pourcentages
F(x) < 0.025	x est très petite	2.5%
0.025< F(x) < 0.15	x est petite	12.5%
0.95< F(x) < F(0.975)	x est grande	12.5%
F(x)>0.975	x est très grande.	2.5%

Tableau 3.2 : seconde règle de classification des valeurs

On ne compare pas ici une valeur x à la moyenne des observations : le raisonnement consiste à dire par exemple que quelqu’un, de taille x, est très grand parce que la plupart des gens sont plus petits que lui (F(x) >0.975) ou encore parce que peu de gens sont plus grands que lui.

L’avantage de cette règle par rapport à la première est de donner toujours des résultats cohérents avec les observations.

Exemple : on donne dans le tableau 6.1 du chapitre 1 la liste des achats classés par valeur croissante. Il est facile d’en déduire un classement des achats :

Achats d’un montant très faible (2.5% de 50, 1 valeur) : x₅

Achats d’un montant faible (12.5% de 50, 6 valeurs) : x₂₈, x₄, x₃, x₂₉, x₃₀, x₃₁

Achats d’un montant élevé (12.5% de 50, 6 valeurs) : x_9, x₈, x₁₂, x₁₁, x₃₉, x₃₇

Achats d’un montant très élevé (2.5% de 50, 1 valeur) : x₂₇

4.3 Concentration

Le coefficient de concentration de Gini. est un paramètre concernant des données positives ou nulles, dont l’interprétation est intéressante en économie et marketing, et qui caractérise « la courbe de concentration ».

Les observations sont classées suivant les valeurs croissantes : on les note comme précédemment x(i), i = 1, …n. L’observation x(1) est donc la plus petite valeur, x(n) la plus grande. Ces observations étant toutes positives, on a x(1) ³ 0.

Au nombre k on associe la somme des k plus petites valeurs x(i), i = 1, …, k..

			k
k	––––––®	S(k) =	S	x(i)
			i = 1

Au nombre n on associe donc la somme des n plus petites valeurs, ou la somme des n valeurs :

			n
n	––––––®	S(n) =	S	x(i)
			i = 1

A la proportion p = k/n, on associe la proportion de la somme des k plus petites valeurs, et l’on définit ainsi la courbe de concentration :

Définition : on appelle courbe de concentration la représentation graphique de la fonction définie par :

p = k/n

–––––®

C(p) =S(k)/S(n)

Exemple numérique : calculons la courbe de concentration dans le cas des données suivantes : x₁= 112, x₂ = 151, x₃ = 210, x₄ = 225, x₅ = 230, x₆ = 354, x₇=360, x₈ = 450. On calcule la somme de toutes les valeurs :

	8
S(8) =	S	xi	= 2092
	i = 1

On a :

p = 1/8	C(p) = 112/2092	= 0.054
p = 2/8	C(p) = (112 + 151)/2092	= 0.126
p = 3/8	C(p) = (112 + 151 + 210)/2092	= 0.226
p = 4/8	C(p) = (112 + 151 + 210 + 225)/2092	= 0.334
p = 5/8	C(p) = (112 + 151 + 210 + 225 + 230)/2092	= 0.444
p = 6/8	C(p) = (112 + 151 + 210 + 225 + 230 + 354)/2092	= 0.613
p = 7/8	C(p) = (112 + 151 + 210 + 225 + 230 + 354 + 360)/2092	= 0.785
p = 8/8	C(p) = (112 + 151 + 210 + 225 + 230 + 354 + 360 + 450)/2092	= 1

D’où la courbe de concentration :

Figure 3.2 : courbe de concentration

(exemple précédent)

On dit qu’il y a équiconcentration quand les k plus petites valeurs, en proportion
p = k/n, représentent la même proportion p de la somme totale quel que soit k :

	k	S(k)
p =	–––	= –––––
	n	S(n)

Cette équiconcentration est caractérisée par la droite y = x représentée sur la figure 4.

Nous admettons ici les propriétés suivantes, certaines étant démontrées dans les compléments pédagogiques du cédérom.

· L’équiconcentration signifie que les observations sont constantes ;

· La fonction C(p) est croissante et égale à 1 pour p = 1 (ou k = n) ;

· C(p) est toujours inférieur à p, ce qui signifie que la courbe de concentration est toujours en dessous de la droite y = x.

· C(p) augmente de plus en plus vite.

Comme on peut le constater sur la figure 4 ci-dessus, l’aire comprise entre la droite
y = x et la courbe de concentration varie de 0 à 0.5. L’usage en statistique étant d’utiliser des paramètres variant de 0 à 1, on définit le coefficient de Gini par le double de cette aire :

Définition : on appelle coefficient de concentration g de Gini le double de l’aire comprise entre la droite y = x et la courbe de concentration.

Son calcul n’est pas simple. On peut utiliser la formule suivante, dans laquelle m est la moyenne des x_i (Saporta, p. 124):

		n	n
		S	S	çxi – xj ç
		i = 1	j = i +1
g	=	–––––––––––––––––––––
		n ( n – 1 ) m

Les propriétés du coefficient de Gini sont les suivantes : :

· Plus le coefficient est proche de 1, plus la somme dépend des observations les plus grandes.

· Plus le coefficient est proche de 0, moins la somme dépend des observations les plus grandes.

Exemple : La courbe de concentration des achats de la clientèle d’Euromarket est donnée en figure 4.

Les 50% plus petits achats représentent à peu près 27% du total des ventes. Il faut considérer les 75% (environ) plus petits achats pour obtenir la moitié du chiffre d’affaire. On peut dire aussi que les 25% clients les plus importants réalisent la moitié du chiffre d’affaires ou encore que le montant de leurs achats est le double de la moyenne.

L’aire totale du carré est égale à 1, et le coefficient de concentration de Gini est le double de l’aire colorée en gris. Il est ici égal à 0.35 : la concentration des achats n’est pas très forte, et la perte de quelques gros clients n’aurait pas d’effet important sur le chiffre d’affaires total.

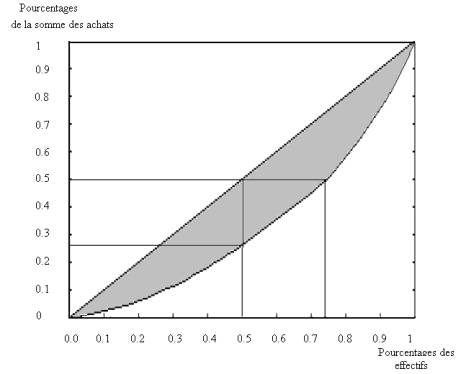
Figure 4.2 : Courbe de concentration

des achats de la clientèle d’Euromarket

Conclusion.

La plupart des tableurs et certaines calculatrices permettent de calculer sans difficulté la moyenne et la variance d’une série d’observations, mais il est préférable d’utiliser un logiciel spécialisé pour calculer les autres paramètres.

La liste que nous avons donnée est limitée aux paramètres les plus classiques. Les résultats donnés par les logiciels ne se limitent pas à cette liste, et donnent des variantes des coefficients d’asymétrie et d’aplatissement ainsi que des paramètres spécifiques à certaines données. Les calculs numériques sont quasiment toujours possibles et les résultats n’ont donc pas toujours de signification, comme le coefficient de concentration lorsqu’il est calculé sur des données prenant des valeurs négatives. Il faut donc effectuer le tri des résultats et se limiter à examiner les paramètres adaptés aux données et dont on connaît le sens.

Table des matières

1. Caractéristiques de tendance centrale. 2

1.1 Notion de distance. 2

1.2 Caractéristiques de tendance centrale ; médiane, moyenne. 2

2. Caractéristiques de dispersion. 5

2.1 Ecart absolu moyen, variance et écart-type. 5

2.2 Comparaison d’une valeur à la moyenne. 7

2.3 Valeurs centrées réduites. 8

3. Autres paramètres. 9

3.1 Coefficient de variation. 9

3.2 Coefficients de forme. 10

4. Fonction de répartition. quantiles. 12

4.1 Fonction de répartition. 12

4.2 Quantiles, quartiles, déciles ... 15

4.3 Concentration. 17

Conclusion. 20

---

[1] La médiane était utilisée dans les compétitions sportives avant l’utilisation du chronométrage électronique. La valeur choisie était la médiane des mesures effectuées par les trois chronométreurs, pour éviter les erreurs dues à un déclenchement tardif ou anticipé du chronomètre.