7. A.c.p. dES DONNéES EUROMARKET.
On considère l’échantillon de 50 clients de l’hypermarché Euromarket dont on connaît l’âge, le revenu, le montant des achats et le nombre d’enfants (données).
1) On considère les clients de rangs 1 et 2 :
|
ind. |
âge |
revenu |
achats |
nombre d’enfants |
|
1 |
51 |
195888 |
150.15 |
3 |
|
2 |
39 |
128456 |
173.12 |
2 |
Le détail du calcul du carré de la distance est donné dans le tableau suivant :
|
Variables centrées réduites |
ind. 1 |
ind. 2 |
carré de la différence |
pourcentage de la distance totale |
|
X1 |
1.171 |
-0.113 |
1.6503 |
21.20% |
|
X2 |
2.980 |
0.703 |
5.1842 |
66.61% |
|
X3 |
-0.805 |
-0.694 |
0.0123 |
0.16% |
|
X4 |
1.142 |
0.174 |
0.9367 |
12.03% |
|
Sommes |
|
|
7.7835 |
100% |
|
Distance totale : d(1,2)2 = 7.7835 |
2) Le nombre d’axes principaux que l’on peut calculer est égal au nombre de variables considérés, lui-même égal à la somme des valeurs propres :
|
l1 + l2 + l3 + l4 = 4 |
La variance de la quatrième composante principale est la valeur propre l4. On a évidemment :
l4 = 4 – (l1 + l2 + l3) = 0.280
|
l4 = 0.280 |
3) Le cercle des corrélations donne la représentation graphique des variables sen fonction de leurs coefficients de corrélation avec les composantes principales :
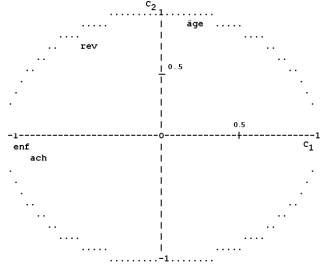
Cercle de corrélation C1 x C2
On constate la liaison entre le montant des achats et le nombre d’enfants et la non corrélation avec le revenu et l’âge. La première composante principale reflète la consommation, tandis que le second la situation sociale.
4) Le plan principal 1 x 2 est donné en annexe :
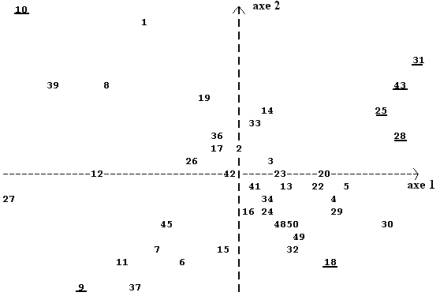
Plan principal 1 x 2
Les clients n° 31, 43, 25, 28 ont dépensé une somme relativement faible malgré un revenu élevé ; on peut l’expliquer par leur âge, nettement plus élevé que la moyenne des clients observés. Le client n° 10 est particulier : sa composante principale c1 très faible montre que ses dépenses sont élevées, qu’il a de nombreux enfants, et sa composante principale c2 qu’il bénéficie d’un revenu élevé qu’il est relativement âgé. Le client n° 18 présente exactement les caractéristiques inverses, tandis que le client n° 9, jeune et à faible revenu, a effectué des achats relativement importants dus peut-être à un nombre d’enfants relativement élevés.
On donne ci-dessous les profils de ces clients :
|
n° |
âge |
revenu |
achats |
enfants |
|
31 |
68 |
86468 |
104.57 |
0 |
|
43 |
67 |
72999 |
241.78 |
0 |
|
25 |
62 |
76865 |
293.12 |
0 |
|
28 |
48 |
96885 |
63.22 |
0 |
|
10 |
57 |
196484 |
555.1 |
4 |
|
18 |
29 |
74036 |
190.65 |
1 |
|
9 |
29 |
84480 |
841.5 |
3 |
5) Les carrés des distances d’(1,2), d’(2,10), d’(1,10) entre les projections des clients de rang 1, 2 et 3 sur le plan 1 x 2 sont données par la somme des carrés des différences de leurs coordonnées sur les axes.
On obtient :
d’(1,2)2 = (–1.286–0.023)2 + (2.822 – 0.464)2 = 7.276
|
Distance sur le plan 1 x 2 : d’(1,2)2 = 7.276 |
On a calculé dans la question 1 la distance exacte entre ces deux clients :
|
Distance totale : d(1,2)2 = 7.783 |
Le rapport d’(1,2)2 / d(1,2)2, égal à 0.93, montre que la distance réelle entre les clients 1 et 2 est presque égale à la distance entre leurs projections sur le plan 1 x 2. On vérifiera que c’est également le cas des clients 1 et 3 (0.95), mais que la distance entre les clients 2 et 3 est moins bien reconstruite (0.59).
Cette reconstruction est globalement satisfaisante, comme le montre le pourcentage d’inertie expliqué par le plan 1 x 2 (78%) : ce pourcentage est le rapport entre la somme des carrés des distances entre les projections sur le plan 1 x 2 et la somme des carrés des distances réelles.