3. Recherche de modèles et désaisonnalisation.
On considère les séries chronologiques trimestrielles suivantes :
|
|
1 |
2 |
3 |
4 |
|
|
1 |
2 |
3 |
4 |
|
1 |
115.9 |
106.1 |
89.5 |
99.3 |
|
1 |
229.8 |
266.1 |
202.8 |
207.9 |
|
2 |
121.2 |
107.8 |
91.3 |
101.5 |
|
2 |
272.1 |
323.8 |
248.6 |
244.9 |
|
3 |
120.1 |
113.5 |
97.0 |
107.0 |
|
3 |
329.8 |
402.9 |
309.8 |
310.8 |
|
4 |
129.5 |
116.6 |
102.5 |
108.4 |
|
4 |
401.8 |
474.3 |
382.1 |
372.7 |
|
5 |
132.4 |
122.3 |
105.5 |
111.8 |
|
5 |
499.6 |
593.5 |
449.7 |
470.5 |
|
6 |
137.5 |
124.0 |
111.9 |
119.6 |
|
6 |
593.2 |
714.8 |
563.8 |
566.6 |
|
|
|
Série |
1 |
|
|
|
|
Série |
2 |
|
I. On suppose que la série 1 suit le modèle additif de période 4.
1) Les moyennes mobiles sont de longueur 4 puisque la période des variations saisonnières est égale à 4. Les valeurs manquantes sont celles des 3e et 4e trimestre de l’année 1, et du 1e et du 2e trimestres de l’année 6.
|
mm1,3 = 103.362 |
mm1,4 = 104.237 |
|
mm6,1 = 120.500 |
mm6,2 = 122.275 |
On donne ci-dessous le calcul détaillé de mm3,4 :
Il s’agit d’une m.m. de longueur paire l = 2 k. la formule est la suivante :
|
mmt |
= |
[0.5
xt–k + xt–k+1 + … + xt–1 + xt + xt+1
+ … + 0.5 xt+k] /
l |
La moyenne mobile mm1,4 correspond à l’instant t = 4. On a l = 4 et par suite k = 2. On a donc :
|
mm4 |
= |
[0.5 x2 |
+ |
x3 |
+ |
x4 |
+ |
x5 |
+ |
0.5 x6] |
/ 4 |
|
|
= |
[0.5 x 106.1 |
+ |
89.5 |
+ |
99.3 |
+ |
121.2 |
+ |
0.5 x 107.8] |
/ 4 |
On obtient la valeur précédente. On dispose maintenant de toutes les moyennes mobiles : la représentation graphique donne la justification demandée.

Représentation graphique de la série 1 (en noir)
et des moyennes mobiles de longueur 4 (en rouge)
La tendance décrite par les moyennes mobiles est visiblement linéaire.
2) On peut donc calculer les coefficients saisonniers en complétant le tableau des différences :
|
|
1 |
2 |
3 |
4 |
|
1 |
|
|
–13.862 |
–4.937 |
|
2 |
16.525 |
2.625 |
–14.012 |
–4.387 |
|
3 |
12.787 |
4.787 |
–13.57 |
–5.137 |
|
4 |
16.287 |
2.525 |
–12.112 |
–7.287 |
|
5 |
15.625 |
4.725 |
–13.137 |
–7.687 |
|
6 |
17.000 |
1.725 |
|
|
Différences entre observations et moyennes mobiles
2) On constate que pour chaque trimestre (c’est-à-dire dans chaque colonne), les différences sont proches les unes des autres sans variation régulière. Cette stabilité confirme le modèle additif dont les coefficients saisonniers sont calculés suivant la procédure suivante :
- on calcule la moyenne de chaque colonne, appelés coefficients saisonniers initiaux :
|
1 |
2 |
3 |
4 |
|
15.645 |
3.2775 |
–13.34 |
–5.8875 |
- on calcule la moyenne m des valeurs obtenues :
m = –0.07625
- on centre les coefficients saisonniers initiaux, pour obtenir les coefficients saisonniers définitifs :
|
s1 |
= |
15.645 – (–0.07625) |
= |
15.72125 |
|
s2 |
= |
3.2775 – (–0.07625) |
= |
3.35375 |
|
s3 |
= |
–13.34 – (–0.07625) |
= |
–13.26375 |
|
s4 |
= |
–5.8875 – (–0.07625) |
= |
–5.81125 |
|
s1 |
s2 |
s3 |
s4 |
|
15.72125 |
3.35375 |
–13.26375 |
–5.81125 |
3) Les observations de l’année 7 sont les suivantes :
|
7 |
138.5 |
126.0 |
119.9 |
129.6 |
Calculer les valeurs désaisonnalisées. Que peut-on dire de la tendance ?
II. On considère maintenant la série 2.
1) La démarche est analogue à la précédente. On commence par représenter graphiquement les observations et les m.m. de longueur 4 :
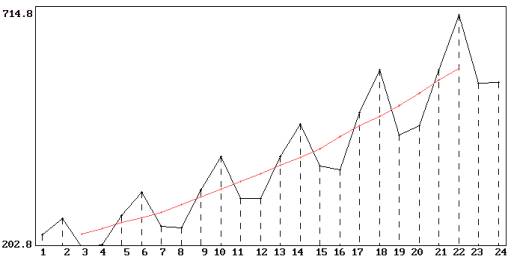
Représentation graphique de la série 1 (en noir)
et des moyennes mobiles de longueur 4 (en rouge)
Les m.m. de longueur 4 font disparaître les variations saisonnières et donnent une approximation initiale satisfaisante de la tendance, qui est évidemment croissante. Les écarts entre les observations et les m.m. augmentent avec la tendance. Le modèle multiplicatif est vraisemblable.
On calcule donc les rapports entre les observations et les moyennes mobiles :
|
|
1 |
2 |
3 |
4 |
|
1 |
|
|
0.874 |
0.850 |
|
2 |
1.057 |
1.209 |
0.889 |
0.825 |
|
3 |
1.049 |
1.220 |
0.891 |
0.850 |
|
4 |
1.048 |
1.185 |
0.909 |
0.833 |
|
5 |
1.062 |
1.208 |
0.873 |
0.868 |
|
6 |
1.038 |
1.196 |
|
|
Rapports des observations aux moyennes mobiles (série 2)
Pour chaque trimestre, ces rapports sont plus ou moins constants , conformément au modèle multiplicatif qui est donc confirmé.
- Les premières approximations des coefficients saisonniers sont données par la moyenne des rapports :
|
1 |
2 |
3 |
4 |
|
1.051139 |
1.204095 |
0.8877224 |
0.8457735 |
- on calcule ensuite la moyenne des valeurs obtenues :
M = 0.9971826
- On divise ensuite chaque coefficient saisonnier initial par cette moyenne, de façon à obtenir des coefficients saisonniers définitifs de moyenne 1 :
|
S1 |
= |
1.051139 / 0.9971826 |
= |
1.054109 |
|
S2 |
= |
1.204095 / 0.9971826 |
= |
1.207497 |
|
S3 |
= |
0.8877224 / 0.9971826 |
= |
0.8902305 |
|
S4 |
= |
0.8457735 / 0.9971826 |
= |
0.8481631 |
|
S1 |
S2 |
S3 |
S4 |
|
1.054109 |
1.207497 |
0.8902305 |
0.8481631 |
2) Le filtre de Buys Ballot peut être utilisé pour analyser une série chronologique suivant un modèle additif et dont la tendance est linéaire. On a vu que ces propriétés ne sont pas vérifiées par la série 2, et l’objectif de l’exercice est de constater les résultats du filtre lorsque les hypothèses nécessaires ne sont pas vérifiées.
|
Coeff. de régression b |
= |
19.12196 |
Coeff.constant |
= |
153.9713 |
|
Coeff. de corrélation r |
= |
0.98597 |
Variance des résidus S² |
= |
538.6254 |
|
s1 |
= |
23.40378 |
s2 |
= |
79.13182 |
|
s3 |
= |
–43.09015 |
s4 |
= |
–59.44545 |
L’année 7 correspond aux instants 25, 26 , 27 et 28.
|
1e trimestre : |
t = 25 |
x25p = 19.12196 x 25 + 153.9713 + 23.40378 = 655.42416 |
|
2e trimestre : |
t = 26 |
x26p = 19.12196 x 26 + 153.9713 + 79.13182 = 730.27416 |
|
3e trimestre : |
t = 27 |
x27p = 19.12196 x 27 + 153.9713 – 43.09015 = 627.17416 |
|
4e trimestre : |
t = 28 |
x28p = 19.12196 x 28 + 153.9713 – 59.44545 = 629.94083 |
|
|
prévisions |
observations |
erreurs |
|
1e trimestre : |
655.42416 |
683.2 |
27.77584 |
|
2e trimestre : |
730.27416 |
788.8 |
58.52584 |
|
3e trimestre : |
627.17416 |
653.8 |
26.62584 |
|
4e trimestre : |
629.94083 |
656.6 |
26.65917 |
On observe que toutes les erreurs sont positives. La méthode choisie donne des prévisions inférieures aux observations pour toute l’année 7.
4) On donne ci-dessous les résidus manquants :
|
e1,1 = 33.303 |
e2,2 = –24.034 |
e4,3 = –15.610 |
e6,4 = 13.147 |
On observe sur la représentation graphique une liaison entre les résidus et le temps : ils sont toujours négatifs au centre de la période étudiée et positifs aux extrémités. Cette liaision n’est pas linéaire, et le coefficient de corrélation entre le temps t et les résidus est égal à 0 : cette propriété découle directement des propriétés du filtre de Buys Ballot, considéré comme une régression linéaire multiple dont les variables explicatives sont le temps et des variables « dichotomiques » définies par
|
X1(t) = 1 |
si t = 1, 5, 9, … |
(1e trimestre), |
X1(t)=0 sinon |
|
X2(t) = 1 |
si t = 2, 6, 10, … |
(2e trimestre), |
X2(t)=0 sinon |
|
X3(t) = 1 |
si t = 3, 7, 11, … |
(3e trimestre), |
X3(t)=0 sinon |
|
X4(t) = 1 |
si t = 4, 8, 12, … |
(4e trimestre), |
X4(t)=0 sinon |
Les résidus sont donc non corrélés aux variables explicatives, en particulier la variable X = t.
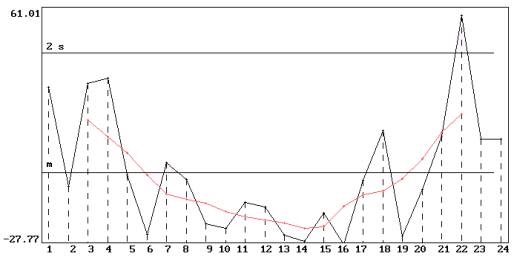
Représentation graphique des résidus (en noir)
et des moyennes mobiles de longueur 4 (en rouge)
Le coefficient de corrélation entre les observations de la série 2 et les valeurs estimées par le filtre de Buys Ballot est égal à 0.9857. Il est très proche de 1, mais cela n’implique pas que l’ajustement soit correct, comme on peut le constater. De même, le coefficient de corrélation entre les résidus et le temps est égal à 0, mais il existe une relation linéaire non linéaire qui montre que le modèle choisi n’est pas le bon.