1. analyse de la tendance par les moyennes mobiles.
On observe ici des propriétés du filtre des moyennes mobiles dont on trouvera la démonstration dans les applications.
On considère les séries chronologiques ci-dessous :
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xt |
102.26 |
103.38 |
102.82 |
103.14 |
103.19 |
104.33 |
103.57 |
103.81 |
105.98 |
106.26 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
xt |
105.26 |
107.18 |
108.04 |
107.86 |
107.80 |
108.41 |
107.80 |
110.78 |
108.12 |
110.69 |
Série X
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
yt |
100.32 |
99.11 |
99.40 |
104.39 |
102.33 |
104.71 |
105.45 |
104.07 |
105.90 |
108.26 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
yt |
108.64 |
109.90 |
110.45 |
112.43 |
113.91 |
116.07 |
116.41 |
119.89 |
120.16 |
123.74 |
Série Y
1) La représentation graphique des deux séries est donnée ci-dessous. Il n’y a pas de variations saisonnières. La tendance de la série X semble linéaire, contrairement à celle de la série Y qui augmente de plus en plus vite. On peut supposer que la série Y est de tendance exponentielle ou polynomiale de degré supérieur ou égal à 2.
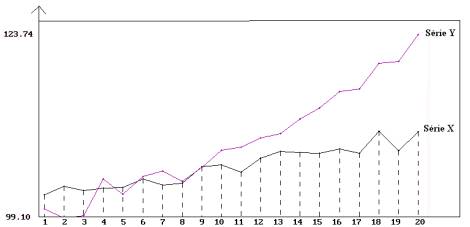
Représentation graphiques des séries chronologiques X et Y
2) Les moyennes mobiles de longueur 5 de la série X sont données ci-dessous :
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xt |
|
|
102.96 |
103.37 |
103.41 |
103.61 |
104.18 |
104.79 |
104.98 |
105.70 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
xt |
106.54 |
106.92 |
107.23 |
107.86 |
107.98 |
108.53 |
108.58 |
109.16 |
|
|
Moyennes mobiles de longueur 5 de la série X
La première moyenne mobile définie correspond à l’instant t = 3, et la dernière à l’instant t = 18.
Les moyennes mobiles de longueur 7 de la série Y sont les suivantes :
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xt |
|
|
|
102.24 |
102.78 |
103.75 |
105.01 |
105.62 |
106.70 |
107.52 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
xt |
108.52 |
109.93 |
111.38 |
112.54 |
114.15 |
115.62 |
117.51 |
|
|
|
Moyennes mobiles de longueur 7 de la série Y
La première moyenne mobile définie correspond à l’instant t = 4, et la dernière à l’instant t = 17.
3) L’ajustement linéaire de la série X donne les résultats suivants :
|
xt = 0.4234181 t + 101.588 |
|
|
r = 0.95121 |
s² = 0.62724 |
On dispose de 20 résidus, dont le coefficient d’asymétrie, égal à –0.176, peut être considéré comme nul puisqu’il est inférieur en valeur absolue à la valeur limite donnée par la table (0.772 pour a = 5% et n = 20). Le coefficient d’aplatissement est égal à 2.298 et est compris entre les valeurs données par la table statistique pour n = 20 (1.820 et 4.170). On peut donc admettre que les résidus sont répartis suivant la loi normale. Le test du T sur le coefficient de régression est donc utilisable, et aboutit au rejet de la nullité de ce coefficient pour un risque de première espèce a = 5% (le t est égal à 13.079, supérieur à la valeur limite 2.10 donnée par la table statistique pour un degré de liberté égal à 18).
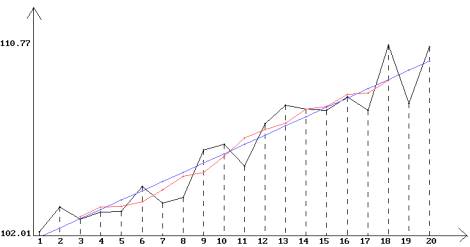
Représentation de la série X, des m.m. de longueur 5
et de la droite de régression.
Pour terminer le contrôle du modèle, on analyse les résidus en les représentant graphiquement :
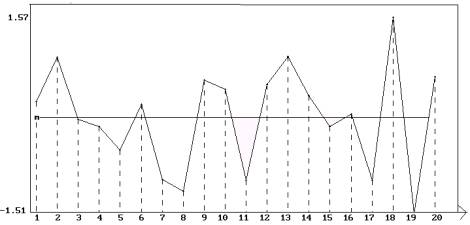
Représentation graphique de la série des résidus
obtenus par ajustement linéaire de la série X.
Ces résidus ne présente aucune particularité et on ne distingue aucune tendance non linéaire.
On peut donc admettre le modèle précédent.
4) On effectue maintenant l’ajustement linéaire de la série Y :
|
yt =1.19827 t + 96.69438 |
s² = 2.228 |
|
r = 0.97745 |
s² = 2.476 |
Le coefficient de corrélation est plus élevé que le précédent. L’ajustement paraît correct numériquement, mais la représentation graphique montre que la droite représente mal la tendance. Les résidus ont pour coefficient d’asymétrie 0.694 et pour coefficient d’aplatissement 2.5277 : ces valeurs sont acceptables pour une loi normale et un risque de première espèce égal à 5%.
C’est en représentant les couples (t, et) que l’on détecte l’inadaptation de la droite pour représenter la tendance : on observe en effet que les résidus sont plus élevés au début et à la fin de la période qu’au centre, ce qui laisse penser qu’une liaison non linéaire peut être plus efficace que l’ajustement linéaire précédent.
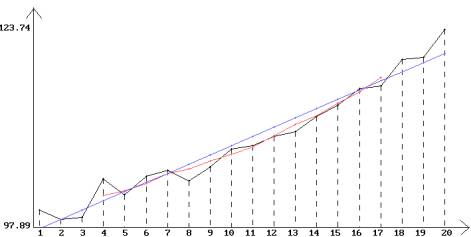
Représentation graphique de la série Y, des m.m. de
longueur 7
et de la droite de régression.
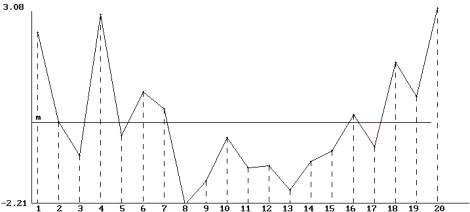
Représentation graphique de la série des résidus
obtenus par ajustement linéaire de la série Y.
On peut donc rechercher un ajustement exponentiel ou par un polynôme. N’ayant aucune raison particulière de choisir une liaison exponentielle, on recherche la liaison la plus simple possible, donc un polynôme de degré 2.
On obtient les résultats suivants :
|
Y = 0.0365 t2 + 0.4312 t + 99.5069 |
S2 = 1.057 |
|
R = 0.9894 |
S’2 = 1.435 |
Le coefficient de corrélation multiple est supérieur au coefficient de corrélation précédent, et la variance des résidus inférieure. C’est toujours le cas lorsqu’une variable explicative supplémentaire est introduite (cf. chap. 7). Par contre, les estimations sans biais de la variance résiduelle montrent que le second modèle est « meilleur » que le premier.
Les coefficients d’asymétrie et d’aplatissement sont égaux à 0.496 et 2.996 : ils ne contredisent pas l’hypothèse de normalité des résidus.
Le T de Student associé au coefficient de régression de t2 est égal 4.340 : il est significativement non nul (la valeur limite pour n = 20 est égale à 2.11 (on admettra que le degré de liberté est égal à n = 20 – 2 – 1 = 17).
Les résidus ne présentent plus de tendance particulière. On peut donc admettre que ce modèle est satisfaisant, et qu’il est par suite inutile de chercher une ajustement par un polynôme de degré 3.
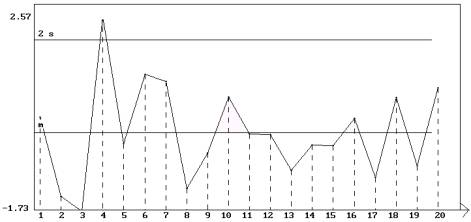
Représentation graphique de la série des résidus
obtenus par ajustement polynomial de degré 2