11. Histogramme et paramètres de données continues.

1) Le tableau ci-dessous donne la densité :

Borne inf.	Borne sup.	Effect.	Longueur de l’intervalle.	Densité
0	10	16	10	0.0111
10	20	16	10	0.0111
20	25	16	5	0.0222
25	30	16	5	0.0222
30	40	16	10	0.0111
40	60	16	20	0.0056
60	80	16	20	0.0056
80	100	16	20	0.0056
100	150	16	50	0.0022

On remarque évidemment que les effectifs des classes sont égaux, alors que leurs longueurs sont inégales. Il y a ici 9 classes de même effectif représentant chacun 11% de l’effectif total. Le calcul de la densité dans la classe 1 est le suivant :

longueur de l’intervalle :	l =10
proportion observée de valeurs dans cet intervalle :	p = 16 / 144
densité d = p / l	d = (16 / 144) / 10 = 0.011

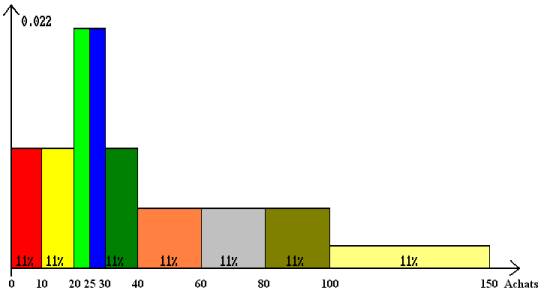
Histogramme des achats (144 valeurs, 9 classes)

La valeur limite des coefficients d’asymétrie est donnée par la table, mais l’effectif n = 144 n’y figure pas. En prenant comme effectif 150, la règle est la suivante pour a = 5% :

- ú c_as ú < 0.321 l’histogramme est à peu près symétrique

- ú c_as ú >0.321 l’histogramme n’est pas symétrique

Le coefficient d’asymétrie est égal à 0.799 : l’histogramme ne peut pas être considéré comme symétrique. Il est largement positif, conformément à la forme de l’histogramme. Il n’est pas utile d’étudier le coefficient d’aplatissement puisqu’on sait que l’histogramme est non symétrique et donc différent de la courbe en cloche.

2) La moyenne est évidente à calculer :

m = 7040 / 144 = 48.89

La variance est égale à la moyenne des carrés moins le carré de la moyenne. Il est mieux d’effectuer les calculs complètement à la calculatrice au lieu de reprendre la moyenne obtenue ci-dessus :

s² = 541 800 / 144 – (7040 / 144)²

On trouve finalement :

Moyenne	Variance	Ecart-type
m = 48.89	s^2 = 1372.376	s = 37.05

Le coefficient de variation est le rapport de l’écart-type à la moyenne exprimé en pourcentage. On trouve :

c_v = 76%

Les observations sont de l’ordre de 49 ± 76%. On notera toutefois ici que cette expression est abusive puisque la répartition est différente de la loi normale.

Pour trouver la médiane, on compte les observations dans chaque classe, en commençant par la première :

	nombre d’observations	pourcentage
£ 0	0	0%
£ 10	16	11%
£ 20	32	22%
£ 25	48	33%
£ 30	64	44%
£ 40	80	55%
£ 60	96	66%
£ 80	112	77%
£ 100	128	88%
£ 1500	144	100%

La médiane correspond à un pourcentage de 50%, soit le centre de l’intervalle [44%, 55%). On choisit donc le centre de l’intervalle [30, 40) c’est-à-dire 35.

mé = 35

Le calcul précédent peut être arrêté dès qu’on a dépassé les 50% si l’on ne cherche que la médiane. On a en fait calculé la fonction de répartition, représentée ci-dessous. L’interpolation linéaire consiste à joindre les points par des segments de droite.

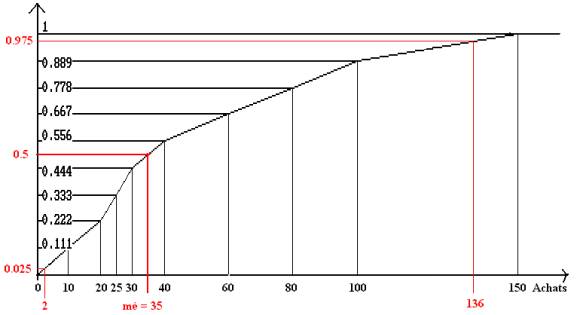
Fonction de répartition des achats
(interpolation linéaire)

3) Un client a acheté pour 92 euros de marchandises. La valeur centrée réduite de son achat est égale à :

x = 92 €

x’ = (x – m ) / s

= (92 – 48.89) / 37.05.

On trouve

x’ = 1.16.

La valeur centrée réduite est supérieure à 12, ce qui signifie que l’écart entre la valeur initiale x et la moyenne m est compris entre m et m + s. L’achat est important.

Pour x 5 €, on trouve :

x’ = – 1.18

Il s’agit donc d’un montant faible.

Les achats très faibles sont inférieurs d’après la règle à la valeur m – 2 s. Or :

m – 2 s = 48.89 – 2 x 37.05 = -25.21 €

On trouve une valeur négative, ce qui n’a pas de sens : la règle fondée sur la moyenne et l’écart-type fonctionne mal ici, et cela s’explique par l’asymétrie de l’histogramme : il n’y a pas de très petites valeurs suivant la règle. On utilise donc une façon de procéder, fondée sur les quantiles : la règle, précisée dans le cours, consiste à considérer comme très petites les 2.5% plus petites valeurs et comme très grandes les 2.5% plus grandes. On trouve graphiquement ces valeurs (2 et 136) comme c’est indiqué sur la fonction de répartition.