3. Autres méthodes.

Il existe beaucoup d’autres méthodes d’analyse de données multidimensionnelles : analyse canonique, analyse factorielle des correspondances multiples, … Nous en présentons rapidement deux autres fréquemment utilisées en techniques de commercialisation : l’analyse factorielle discriminante et la classification.

3.1 Analyse factorielle discriminante.

L’analyse factorielle discriminante établit la relation entre les groupes d’unités statistiques définis par une variable qualitative et plusieurs variables quantitatives. Elle présente la particularité de proposer une règle de classement des unités statistiques.

Exemple : nous avons constitué trois groupes de clients d’Euromarket : les clients sans enfants (groupe 1), les familles classiques ayant 1 ou deux enfants (groupe 2) et les familles nombreuses (3 ou 4 enfants). La question à laquelle l’analyse factorielle discriminante permet de répondre concerne la liaison entre les groupes de famille (sans enfants, classiques, nombreuses), et les variables quantitatives observées (revenu, montant des achat, âge). L’objectif final est d’affecter un client supplémentaire à un groupe de familles suivant ses caractéristiques.

La méthodologie est fondée sur la décomposition de la variance lorsque les unités statistiques sont réparties en plusieurs groupes. C’est une propriété que nous avons déjà vue précédemment (chapitre 7, paragraphe 2.2), que nous rappelons rapidement :

Soit X une variable statistique observée sur n unités statistiques réparties en k groupes I₁, I₂, …, I_l, … I_k., d’effectifs n₁, n₂, …, n_l, … n_k. Le nombre total d’observations est égal à n :

n = n₁ + n₂ + … + n_l + … n_k

On note m et s² la moyenne et la variance de la variable X dans la totalité de la population et m₁, m₂, …, m_l, …, m_k et s₁², s₂², …, s_l², …, s_k² dans chaque groupe. On a alors les relations ci-dessous :

–––

n_l m_l

s²

–––

n_l (m_l – m)²

–––

n_l s_l²

l = 1

La seconde formule exprime la variance totale (s²) comme la somme de la variance « inter » (premier terme : variance des moyennes pondérées) et de la moyenne des variances « intra » (second terme).

Lorsque les groupes sont très différents les uns des autres, la variance inter est élevée relativement à la variance totale, et les variances intra sont faibles, ce qui signifie qu’au sein d’un groupe donné, les unités statistiques sont proches de la moyenne de ce groupe. Inversement, si les groupes sont mélangés, cela signifie que les moyennes sont relativement proches les unes des autres, et que les observations d’un même groupe sont fortement dispersées. On mesure cette « discrimination » par le rapport de corrélation :

Définition : on appelle rapport de corrélation le rapport de la variance inter à la variance totale.

Ce rapport est toujours compris entre 0 et 1. Ses propriétés sont les suivantes :

· plus il est proche de 1, plus la variance inter est élevée, plus les variances intra sont faibles (par rapport à la variance totale) et plus forte est la discrimination.

Figure 7.9 : rapport de corrélation proche de 1, bonne discrimination

· plus il est proche de 0, plus la variance inter est faible, plus les variances intra sont élevées, et moins la discrimination est forte.

Figure 8.9 : rapport de corrélation proche de 0, mauvaise discrimination

Pour en apprécier la taille, on peut l’interpréter approximativement comme le carré d’un coefficient de corrélation linéaire (il existe un test d’égalité à 0 fondé sur la loi de Fisher Snedecor).

Cette propriété est vraie quelle que soit la variable quantitative considérée X. Lorsque l’on dispose de plusieurs variables X₁, X₂, …, X_j, …, X_p que l’on suppose centrées réduites, on peut donc considérer l’ensemble des variables Y de la forme :

Y =u₁ X₁ + u₂ X₂ + … + u_j X_j + … + u_p X_p

les coefficients u₁, u₂, …, u_j, …, u_p étant des nombres réels quelconques.

L’analyse factorielle discriminante consiste à chercher ces coefficients de façon que le rapport de corrélation de Y soit le plus élevé possible. Les valeurs moyenne de cette variable Y calculées dans chaque groupe sont les plus dispersées possible au sens de la variance (inter) et inversement les valeurs de Y prises par les unités statistiques de chaque groupe sont concentrées autour de la moyenne de ce groupe (variance intra). La discrimination est maximale. On détermine ainsi la première composante discriminante, dont le rapport de corrélation est appelé pouvoir discriminant.

On cherche ensuite une autre suite de coefficients maximisant le rapport de corrélation, de façon que la seconde composante discriminante soit non corrélée à la précédente et ainsi de suite.

On trouve un nombre de composantes discriminantes inférieur ou égal au nombre de groupes diminué de 1. Parmi ces composantes discriminantes, on ne considère en général que les premières (2 ou 3). Et c’est à l’aide de ces composantes discriminantes que l’on classe les unités statistiques.

3.2 Exemple d’analyse factorielle discriminante.

Les familles clientes d’Euromarket étant réparties en trois groupes suivant le nombre d’enfants, le nombre d’axes discriminants est égal à 2, et la représentation du plan discriminant 1 x 2 est donnée en figure 6.9, chaque client étant représenté par le groupe auquel il appartient.

Le pouvoir discriminant de la première composante discriminante (0.52) n’est que légèrement supérieur au rapport de corrélation du montant des achats (0.46), auquel elle est fortement corrélée (0.893). Celui de la seconde reste relativement élevé (0.25).

On a également représenté les centres de gravité G₁, G₂ et G₃ de ces groupes en éléments supplémentaires – c’est-à-dire qu’ils n’ont pas été pris en compte dans le calcul des axes discriminants.

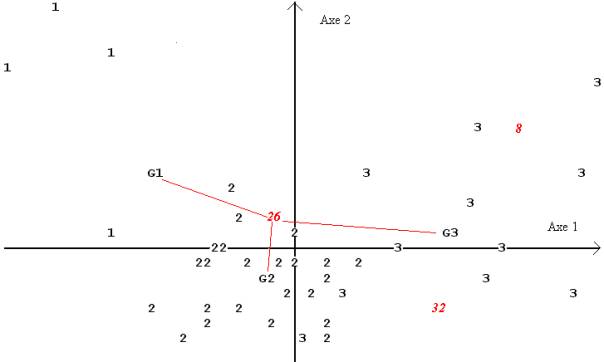
Figure 9.9 : plan discriminant 1 x 2

On note que le groupe 1 est nettement plus âgé en moyenne que les deux autres, que son revenu est légèrement plus faible et que c’est le montant des achats qui différencie le plus le groupe 2 (un ou deux enfants) du groupe 3 (trois ou quatre enfants). On notera que les composantes discriminantes, toujours non corrélées, ne sont pas ici indépendantes : on distingue une liaison non linéaire sur la figure 9.

	effectif	âge	revenu	achats
Groupe 1	6	50.67	87 383.8	209.2233
Groupe 2	31	38.90	107 314.4	238.4945
Groupe 3	13	37.92	117 763.5	553.7369

Moyennes des variables par groupes

(centres de gravité)

La règle d’affectation d’un client à un groupe est la suivante :

· on calcule la distance du client aux centres de gravité des groupes G₁, G₂, G₃.

· on affecte le client au groupe dont le centre de gravité est le plus proche.

On note alors quelques cas particuliers, indiqués par leur rang en italique dans la figure 7.9 : le client 32 appartient au groupe 1, le 8 appartient au groupe 2, le 26 appartient au groupe 3.

D’une façon plus générale, on calcule le tableau donnant la répartition des clients suivant le groupe auquel ils appartiennent (en ligne) et le groupe auquel ils sont affectés (en colonne) :

	1	2	3
1	4	1	1
2	1	28	2
3	0	3	10

Tableau de classement appartenance x affectation

· Sur les six clients du groupe 1, quatre sont bien classés, un est classé dans le groupe 2 et un dans le groupe 3.

· Sur les trente-et-un clients du groupe 2, l’un est classé dans le groupe 1, deux dans le groupe 3.

· Sur les treize clients du groupe 3, trois sont classés dans le groupe 2.

On calcule fréquemment pour résumer ce tableau le pourcentage de bien-classés, égal ici à 84%.

Considérons maintenant un client X âgé de 38 ans, dont le revenu est de 80000F et qui a dépensé 357F. L’analyse discriminante propose de l’affecter dans l’un des trois groupes en fonction de sa distance aux centres de gravité de chaque groupe :

Groupe 1 : 2.601287

Groupe 2 : 0.9520697

Groupe 3 : 3.235366

Ce client est beaucoup plus proche du centre de gravité du groupe 2 que des autres : il a vraisemblablement, d’après l’analyse, un ou deux enfants.

Cette analyse demande toutefois une grande prudence : le nombre d’unités statistiques doit être élevé (50 est la plupart du temps très insuffisant), le nombre de variables faible, et la règle d’affectation à un groupe est discutable.

L’analyse discriminante, comme la régression linéaire, donne des résultats dont la validation est indispensable. Il existe plusieurs façons de contrôler les résultats. La plus simple est d’appliquer la règle choisie sur un échantillon test permettant de comparer le groupe d’affectation au groupe auquel l’u.s. appartient effectivement : il faut disposer pour cela d’un effectif suffisant. Une autre façon est de calculer le pourcentage de bien classés en cas d’affectation aléatoire : on trouve ici 33% en affectant chaque u.s. à un groupe avec la probabilité 1/3. Notons qu’en affectant systématiquement les u.s. au groupe 2 et si les proportions de l’échantillon sont respectées dans la population, le pourcentage de bien classés est égal à 28/50 x 100% = 56%. Ce pourcentage ne mesure donc pas la validité de la règle de façon satisfaisante. C’est pourquoi on peut procéder enfin à une chaotisation de l’échantillon de calcul : on tire au hasard les groupes auxquels sont censés appartenir les observations, et, après avoir effectué l’analyse, on détermine le pourcentage de bien classés. Si ce pourcentage reste du même ordre qu’avec les groupes réels, c’est que la discrimination n’est pas satisfaisante. Nous avons effectué dix fois cette chaotisation et trouvé les pourcentages suivants : 38%, 6%, 24%, 8%, 42%, 24%, 50%, 44%, 24%, 32%. Le pourcentage de 80% est donc satisfaisant (on pourrait augmenter le nombre de chaotisations).

La règle de décision utilisée précédemment est élémentaire : elle n’est justifiée que sous des hypothèses contraignantes (matrice de covariances des groupes constantes). On préfère souvent utiliser comme règle d’affectation l’une de celles que nous donnons dans le paragraphe suivant. On consultera aussi l’application « vers d’autres règles de décision. »Les tests statistiques ne peuvent être utilisés que si les variables considérées suivent la loi normale (ce qui n’est pas le cas dans le fichier EUROMARKET).

3.3 Classification et règles d’affectation.

La classification rassemble des procédures surtout informatiques totalement différentes des analyses factorielles précédentes. Le modèle mathématique est beaucoup moins développé, et les difficultés des méthodes sont surtout algorithmiques et informatiques.

Toutes les procédures de classification suivent la même démarche :

· on compare des objets, qui peuvent être des unités statistiques ou des variables ;

· on définit une notion de distance, qui généralise la notion utilisée en analyse factorielle ;

· on choisit une règle d’affectation d’un objet à un groupe d’objets pour créer des groupes homogènes.

La notion de distance est fréquemment appelée dissimilarité, parce qu’elle ne vérifie pas nécessairement les hypothèses d’une distance mathématique. Les hypothèses qu’elle doit vérifier sont les suivantes :

· la dissimilarité d’un objet à un autre est positive ou nulle ;

· la dissimilarité d’un objet à lui-même est nulle.

Pour rassembler les objets qui se ressemblent, il faut définir la distance entre un objet et un groupe et plus généralement entre deux groupes d’objets. Plusieurs choix pour définir la dissimilarité entre deux groupes sont possibles, parmi lesquels (figure 10.9) :

· la distance la plus petite entre deux objets pris dans chaque groupe ;

· la distance la plus grande entre deux objets pris dans chaque groupe ;

· la distance moyenne entre les objets pris dans chaque groupe ;

· la distance entre les centres de gravité.

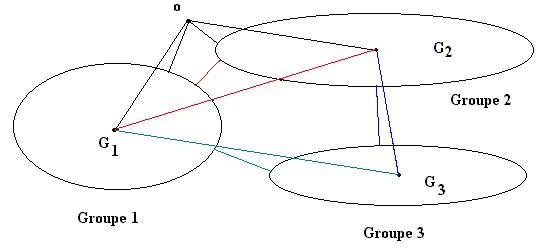
Figure 10.9 : disance entre un objet o et des groupes

distance entre deux groupes

On observe la diversité des proximités suivant le critère choisi ) : l’objet o est affecté au groupe 1 (distance au centre de gravité) ou au groupe 2 (groupe de l’objet le plus proche).

La procédure consiste alors à calculer les distances entre tous les objets, à grouper les deux objets les plus proches pour en constituer un autre qui les remplace, et à recommencer jusqu’à l’obtention d’un seul groupe constitué de tous les objets.

En figure 10.9, suivant la règle choisie, les groupes G₂ et G₃ sont réunis (distance entre les centres de gravité), ou G₁ et G₂ (suivant le plus proche voisin).

La liberté qui est laissée dans le choix de la distance se paie, et la représentation graphique des objets conformément à leurs distances réciproques peut être difficile. En particulier, il n’est pas toujours possible de les représenter géométriquement dans un système d’axes. On utilise souvent pour effectuer cette représentation une arborescence, que l’on appelle aussi dendogramme, analogue à l’arbre de classification des espèces bien connu en biologie.

3.4 Exemple.

Nous avons effectué la classification des clients d’Euromarket en considérant comme distance entre deux clients celle qui est définie par la somme des carrés des différences des variables centrées réduites, comme en analyse en composantes principales, et en choisissant comme critère d’agrégation le critère de minimisation de la variance.

Le dendogramme que l’on obtient est donné en figure 11.9. Il peut être utilisé pour classer les clients en un nombre de groupes fixé, par une procédure appelée troncature. Par exemple, pour un nombre de groupes égal à 4, on obtient la partition suivante :

Classe n° 1	1	8	10	12	25	27	31	39	43
Classe n° 2	2	3	14	16	17	19	21	23	24	26	33	34	35	36	38	41	42	44	47
Classe n° 3	4	5	13	18	2	22	28	29	3	32	4	48	49	5
Classe n° 4	6	7	9	11	15	37	45	46

Partition en 4 classes

Les groupes obtenus n’apparaissent guère sur le plan principal que nous avons donné en figure 3.9. La distance considérée est la même, mais sur ce plan n’apparaissent que les distances reconstruites par les deux premiers axes : cela explique la différence.

Cela explique aussi que souvent, on préfère effectuer cette classification sur les composantes principales ou les facteurs préalablement sélectionnés. On retrouve des groupes cohérents avec l’analyse factorielle.

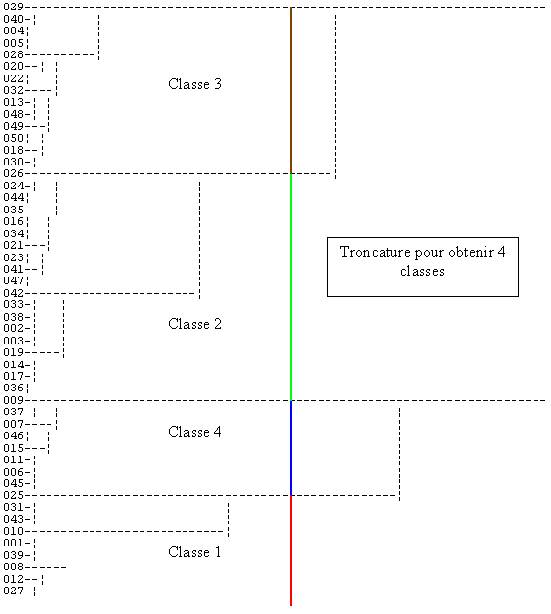
Figure 11.9 : dendogramme des clients d’Euromarket

(distance euclidienne sur les données centrées réduites,

agrégation suivant la variance minimale)