4. Lissage exponentiel.

4.1 Généralités sur le lissage exponentiel.

Le lissage exponentiel est une classe de méthodes de lissage de séries chronologiques dont l'objectif est la prévision à court terme. Ces méthodes sont fondées sur une hypothèse fondamentale : chaque observation à l’instant t dépend des observations précédentes et d'une variation accidentelle, et cette dépendance est plus ou moins stable dans le temps.

L'estimation x_t^p de la série à l’instant t connaissant x_t-1 est donc obtenue par une formule de la forme :

x_t^p = a_t-1 x₀ + a_t-2x₁ + a_t-3 x₂ + …. + a₀ x_t-1

On peut généraliser cette formule au cas où seule l'observation x_t-h est connue :

x_t^p = a_t-h x₀ + a_t-h-1 x₁ + a_t-h-2 x₂ + …. + a₀ x_t-h

Dans le premier cas, on peut prévoir à l’horizon 1 : sachant x_t, on prévoit x_t+1, l'observation suivante, et dans le cas général, on peut prévoir à l'horizon h : sachant x_t, on prévoit x_t+h. On peut penser que plus l'horizon h est faible, meilleure est la prévision.

Les méthodes de lissage exponentiel consistent à choisir les coefficients a_j en fonction de la série étudiée.

· Dans le cas où la série est stationnaire (on ne distingue pas de tendance à la hausse ni à la baisse), on utilise le lissage exponentiel simple. Les coefficients a_j sont de la forme :

a_j = a^j / (1 – a)

où a est la constante de lissage choisie de façon empirique entre 0 et 1. La valeur 1/a est parfois appelée âge moyen du lissage.

· Lorsque la série présente une tendance linéaire par morceaux (la tendance peut être considérée comme linéaire sur une suite de quelques observations), et n'est soumise à aucune variation saisonnière, on effectue les prévisions à l'aide du double lissage exponentiel. En effet, en appliquant deux fois le lissage exponentiel simple, on détermine une suite de droites de tendance qui ajustent les observations.

· Dans le cas d’une série soumise à des variations saisonnières, on utilise souvent le modèle de Holt et Winters, que nous expliquons rapidement dans le paragraphe 4.2.

Dans les lissages exponentiels simple et double, il y a donc une seule constante à fixer. Le choix peut être empirique, c’est-à-dire effectué par l’utilisateur en fonction de la connaissance qu’il a de la série. Lorsque la valeur x_t ne dépend guère que des 3 ou 4 dernières observations, on peut choisir la constante a proche de 1. Inversement, si les observations antérieures gardent longtemps une influence sur la valeur x_t, on choisira a proche de 0. On peut aussi déterminer la constante de façon à minimiser la somme des carrés des erreurs commises pour l’horizon h fixé. Certains programmes proposent cette option.

Exemple : la figure 9.8 ci-dessous montre l'ajustement obtenu à l'horizon 1 du cours de l’action Alcatel par un double lissage exponentiel.

Figure 9.8 : cours du titre Alcatel et prévision à l’horizon 1

par double lissage exponentiel (a = 0.65)

La constante de lissage a été déterminée de façon à minimiser la somme des carrés des erreurs (a = 0.65). La valeur prévue suit la série avec retard.

Le cours prévu à l’instant t = 46 (8 mars 1999) est égal à 122.22 € ; le cours moyen observé de la séance est de 118 € : la prévision n’est pas très satisfaisante. Les méthodes de prévision ne donnent pas de bons résultats sur les cours en Bourse (sinon, cela se saurait !).

4.2 Modèle de Holt et Winters.

La méthode de Holt et Winters permet en effet d'effectuer des prévisions sur des séries chronologiques assez irrégulières et soumises ou non à des variations saisonnières suivant un modèle additif ou multiplicatif.

Elle consiste en trois lissages exponentiels simultanés. On définit donc trois paramètres, notés a, b et g. A chaque instant t, elle donne une estimation :

· de la tendance

· du coefficient saisonnier correspondant

· de la valeur observée.

On peut choisir les coefficients arbitrairement : faibles si l'on considère que la valeur à l’instant t dépend d'un grand nombre d'observations antérieures, élevés dans le cas contraire. On peut aussi en calculer les valeurs optimales, en minimisant la somme des carrés des différences entre les valeurs observées et estimées. On procède ensuite aux prévisions, en considérant que la tendance suit un modèle linéaire additif ou multiplicatif à très court terme.

Exemple : on étudie ici la série constituée du nombre trimestriel de naissances dans la région Centre. La figure 10.8 montre une tendance assez irrégulière, avec des variations saisonnières de période 4.

Le filtre de Buys-Ballot n'est visiblement pas adapté dans ce cas particulier, et nous appliquons ici le modèle de Holt et Winters. Nous choisissons comme modèle un modèle dont la tendance à court terme est linéaire (ici, on se limite à examiner une succession de quelques points), et les variations de période 4 additives. Nous fixons l'horizon à 4 pour disposer des prévisions de toute l'année 1986.

Figure 10.8 : nombre de naissances dans la région Centre de 1972 à 1985

Moyennes mobiles de longueur 4.

Les paramètres optimaux que l'on obtient en minimisant la somme des carrés de la totalité des résidus sont : a = 0.9, b = 0.9, g = 0.1.

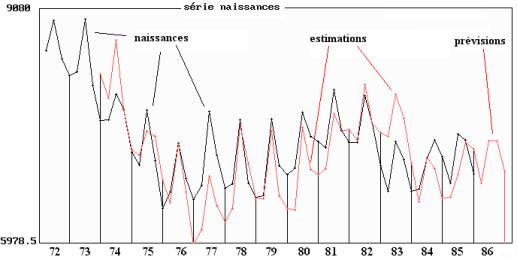
Figure 11.8 : nombre de naissances dans la région Centre de 1972 à 1985

Estimations par le modèle de Holt et Winters et prévision pour 1986

Le tableau 10.8 permet de comparer prévisions et observations de l'année 1986 : les naissances aux deux premiers trimestres ne sont pas très bien estimées, contrairement aux deux dernières.

	1^ertrimestre	2^e trimestre	3^e trimestre	4^e trimestre
observations	7018	7720	7415	6986
prévisions	6824	7410	7405	6984

Tableau 10.8 : nombre de naissances dans la région Centre observés et prévus en 1986