1. Description d'une série chronologique.

On distingue en général trois effets constitutifs d’une série chronologique :

· Un effet à long terme, appelée tendance (on ajoute parfois à long terme), composante tendancielle ou trend ;

· Un effet dit saisonnier, qui réapparaît à intervalles réguliers ; cet effet se traduit par une composante de la série appelée composante saisonnière.

· Un effet inexpliqué : cet effet, que l'on suppose en général dû au hasard, se manifeste par des variations accidentelles.

Dans les séries économiques longues, on cite souvent un effet supplémentaire : c'est ce que l'on appelle le cycle de Kondratiev, qui résulte du fait que, suivant la théorie de Kondratiev, à une période de prospérité économique succède mécaniquement une période de dépression.

1.1 Description de la tendance.

La description initiale de la tendance repose sur l'interprétation de la représentation graphique de la série.

Définition : on appelle tendance (ou variation à long terme ou trend) de la série x_t la série c_t résultant de la totalité des effets permanents auxquels est soumise la série x_t.

Exemple : Nous donnons ci-dessous les cours (en €) du titre Alcatel de code sicovam 13000 du 4 janvier (n°1) au 5 mars 1999 (n°45). L'unité de temps est le jour boursier, et le cours est déterminé par l’offre et la demande elles-mêmes déterminées par l’évolution économique. Les données figurent sur le site (paramètres Alcatel.par) :

1	109.500	10	103.750	19	100.100	28	94.000	37	99.950
2	113.200	11	105.400	20	101.800	29	94.600	38	103.150
3	119.700	12	101.175	21	102.450	30	96.425	39	101.250
4	122.350	13	101.100	22	100.600	31	94.025	40	98.450
5	122.900	14	100.150	23	99.200	32	95.350	41	97.550
6	118.250	15	96.050	24	99.200	33	94.175	42	100.000
7	113.550	16	96.950	25	94.375	34	96.600	43	107.050
8	107.700	17	101.000	26	96.350	35	97.250	44	112.900
9	107.400	18	103.000	27	97.250	36	98.500	45	117.400

Tableau 1.8 : Cours du titre Alcatel du 4 janvier 1999 au 5 mars 1999

La tendance peut être décomposée en trois phases (figure 1.8) :

· Le cours baisse du début des observations (7 janvier ) jusqu'à l'observation n°15 (c'est-à-dire le 22 janvier) ;

· De l'observation n°16 (25 janvier) à l'observation n°41 (1^er mars), le cours diminue légèrement ;

· Il augmente rapidement à partir du 2 mars.

On ne distingue pas sur la figure 1.8 de variations apparaissant à intervalles réguliers : la série n'est soumis à aucun effet saisonnier visible. La composante accidentelle est visualisée par les petites variations de cours d'un jour à l'autre. Par exemple le cours n°11 est supérieur au cours n°10 : cela ne remet pas en cause la baisse de la tendance compte tenu des cours du 7 au 22 janvier.

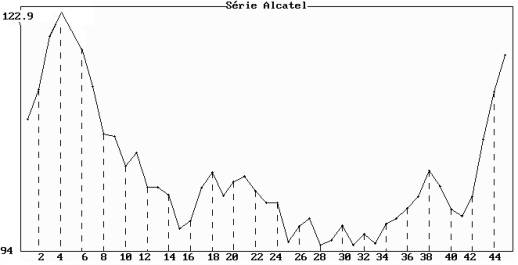
Figure 1.8 : cours journalier du titre Alcatel

(du 4 janvier 1999 au 5 mars 1999)

Pour faire apparaître plus clairement la tendance, il faut atténuer la composante accidentelle. On utilise pour cela les moyennes mobiles définies de la façon suivante :

Définitions :

· on appelle moyenne mobile centrée de longueur impaire l_i = 2 k +1 à l’instant t la valeur moyenne mm_t des observations x_t-k, x_t-k+1, …, x_t, x_t+1, …, x_t+k :

mm_t = (x_t-k + …+ x_t-1 + x_t + x_t+1 + … + x_t+k) / l_i

· on appelle moyenne mobile centrée de longueur paire l_p = 2 k à l’instant t la valeur moyenne mm_t des observations x_t-k, x_t-k+1, x_t-k+2, x_t, x_t+1, …, x_t+k , la première et la dernière étant pondérées par 0.5 :

mm_t = (0.5 x_t-k + x_t-k+1 + … + x_t-1 + x_t + x_t+1 + … + x_t+k-1+ 0.5 x_t+k) / l_p

Dans la première formule, le nombre de termes de la somme est égal à 2 k + 1 : il s'agit bien d'une moyenne. Dans la seconde, la somme des coefficients est égale à 2 k, puisque le premier et le dernier sont égaux à 0.5 : il s'agit d'une moyenne pondérée. Dans les deux cas, le nombre d'observations prise en compte avant l’instant t est égal au nombre d'observations prises en compte après l’instant t : c’est pour cela que les moyennes sont dites centrées.

La première valeur d’une moyenne mobile de longueur 4 ( = 2 x 2) ou 5 (= 2 x 2 + 1) que l’on peut calculer, est à l’instant t = 3, puisque la première observation connue est x₁ :

mm3 = (0.5 x1 + x2 + x3 + x4 + 0.5 x5) / 4	(l = 4)
mm3 = (x1 + x2 + x3 + x4 + x5) / 5	(l = 5)

De façon générale, ne peut calculer de moyenne mobile en t = 1, t = 2, …, t = k puisque les formules ne peuvent être appliquées que si l'on connaît x_t-k. De même, si T est le nombre total d'observations, on ne peut calculer mm_T, … mm_T-k+1 puisqu'il faut connaître x_t+k.

L’avantage des moyennes mobiles est d'atténuer la composante accidentelle tout en conservant les tendances linéaires : la série est dite « lissée », et est d'autant plus lissée que la longueur de la moyenne mobile est élevée comme on peut le constater sur la figure 3.8 sur laquelle nous avons représenté les moyennes mobiles de longueur 14.

Exemple : nous donnons dans le tableau 2.8 un extrait des moyennes mobiles de longueur 5 et les représentations graphiques sur les figures 2.8 et 3.8 des cours du titre Alcatel et des moyennes mobiles de longueur 5 et 14.

Instant	cours (€)	moyenne mobile	Instant	cours (€)€	moyenne mobile
1	109.50000		42	100.00000	103.19000
2	113.20000		43	107.05000	106.98000
3	119.70000	117.53000	44	112.90000
4	122.35000	119.28000	45	117.40000

Tableau 2.8 : cours du titre Alcatel du 4 janvier (n°1) au 5 mars 1999 (n°45)

moyennes mobiles de longueur 5 (extrait)

On notera que, dans les journaux financiers, les moyennes mobiles ne sont pas centrées : on utilise les moyennes des 50 ou 100 dernières observations avant l’instant t pour définir la tendance à l’instant t.

L'inconvénient des moyennes mobiles de longueur 14 est qu’elles ne sont définies qu'à partir de la 8^e observation et jusqu’à la 38^e. On ne dispose d'aucune information sur la tendance ni au début ni à la fin de la période d'observation. Il faut donc choisir la longueur des moyennes mobiles suivant le nombre d'observations et l'objectif de l'analyse. Nous verrons que la longueur de ces m.m. dépend aussi de la période des variations saisonnières pour faire apparaître la tendance.

Figure 2.8 : cours du titre Alcatel du 4 janvier au 5 mars 1999

Moyennes mobiles de longueur 5.

Figure 3.8 : cours du titre Alcatel du 4 janvier au 5 mars 1999

Moyennes mobiles de longueur 4.

Théorème : si la tendance d’une série chronologique x_t est linéaire et a pour équation c_t = b t + a, les moyennes mobiles centrées ont pour tendance la même droite et en sont d’autant plus proches que la longueur des moyennes mobiles est élevée.

Ce théorème est démontré dans un complément pédagogique. Il peut être complété par l’étude de tendance de la forme c_t = b₂t² + b₁t + a proposée en application pédagogique.

1.2 Description simultanée des variations saisonnières et de la tendance.

Une variation saisonnière est caractérisée par le fait qu'elle se produit à intervalles de temps réguliers, d'où d'ailleurs le terme saisonnier.

Définition : on appelle variation saisonnière d'une série chronologique à l’instant t une variation due à un effet momentané se reproduisant régulièrement dans le temps.

Exemple : nous étudions la série chronologique suivante observée trimestriellement pendant 6 ans (tableau 3.8).

	1^er trimestre	2^e trimestre	3^e trimestre	4^e trimestre
Année 1	89.658	97.593	108.906	114.157
Année 2	96.205	99.399	112.763	119.185
Année3	99.602	105.192	116.556	121.911
Année 4	103.272	109.644	121.208	126.508
Année 5	105.637	113.428	125.641	131.147
Année 6	111.118	117.215	129.776	133.000

Tableau 3.8 : série chronologique 1

(période p = 4)

L’observation de chaque trimestre est soumis à un effet particulier qui revient tous les ans ; il y a donc 4 variations saisonnières correspondant chacune à un trimestre.

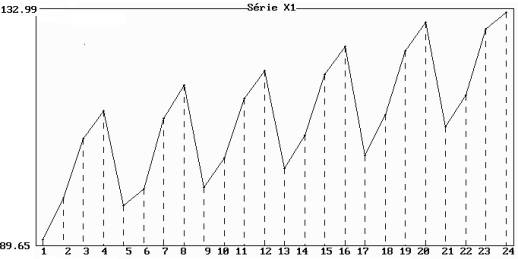
Figure 4.8 : représentation graphique de la série 1

(données observées trimestriellement pendant 6 ans)

Définition : la période notée p des variations saisonnières est la longueur exprimée en unités de temps séparant deux variations saisonnières dues à un même phénomène.

Remarque : nous supposerons dans la suite que la série est soumise à des variations saisonnières de même période p. La période est alors le nombre de variations saisonnières. Cette hypothèse n’est pas toujours réalisée au départ : les ventes par tranches horaires d’un hypermarché sont soumises par exemple à une première variation saisonnière due à l’heure et à une seconde due à la journée. Ce cas est traité théoriquement en considérant une période égale au plus petit commun multiple des deux périodes : deux variations saisonnières de périodes 4 et 6 donnent une variation saisonnière de période 12 (= 3 x 4 = 2 x 6).

Il n'est pas toujours facile de distinguer la tendance lorsque la série chronologique est soumise à des variations saisonnières. La méthode mathématique consiste à calculer les moyennes mobiles en choisissant comme longueur la période des variations saisonnières, de façon à les faire disparaître. Si la moyenne mobile choisie est de longueur différente, les variations saisonnières ne sont pas toujours éliminées (cf. figures 5.8 et 6.8).

Ces moyennes mobiles ont en outre l'avantage d'atténuer les variations accidentelles comme nous l'avons vu précédemment, mais l'inconvénient de n'être définies ni au début ni à la fin de la période observée.

Exemple : on pourra comparer sur les figures 5.8 et 6.8 ci-dessous les moyennes mobiles de longueur 4 (dont les valeurs numériques sont données dans le tableau 4.8) et de longueur 5.

Figure 5.8 : représentation simultanée de la série 1

et des moyennes mobiles de longueur 4

Figure 6.8 : représentation simultanée de la série 1

et des moyennes mobiles de longueur 4

Contrairement aux m.m. de longueur 4, les m.m. de longueur 5 n’éliminent pas les variations saisonnières.

Théorème : les moyennes mobiles d’une série soumise à des variations saisonnières de période p ne sont pas soumises à ces variations saisonnières si leur longueur l est égale à la période p, et plus généralement si leur longueur est un multiple de la période.

Ce théorème est démontré dans un complément pédagogique.

Conclusion : les moyennes mobiles d’une série chronologique dont la tendance est linéaire et les variations saisonnières sont de période p font apparaître la tendance et disparaître les variations saisonnières si leur longueur l est égale à la période p.