3. Filtre de Buys-Ballot.
Le filtre de Buys-Ballot concerne les séries chronologiques suivant un modèle additif et dont la tendance est linéaire. Il consiste à estimer les paramètres de ce modèle suivant le critère des moindres carrés, et permet ensuite, dans la mesure où les hypothèses sont respectées, d'effectuer des prévisions. Il s’agit en fait d’une régression linéaire multiple particulière.
Lorsque la série suit le modèle multiplicatif et que la tendance est exponentielle, les logarithmes des observations vérifient les conditions précédentes. On peut alors appliquer le filtre de Buys-Ballot.
3.1 Filtre de Buys-Ballot.
Nous supposons donc que la série étudiée suit le modèle additif et que la tendance est linéaire :
ct = b t + a
Pour exprimer la tendance en fonction de la ligne i et de la colonne j du tableau, nous utilsons la relation et les variables t, i et j données précédemment :
t = (i-1) p + j
dans laquelle i varie de 1 à n, j de 1 à p. Le nombre total T d'observations est égal à n p.
Le modèle complet est le suivant :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j
= b [(i-1) p + j ] + a + sj + ei,j |
Les coefficients en caractères grecs sont des coefficients théoriques qu’il s’agit d’estimer : on retrouve ici la notation employée dans le chapitre précédent. Les observations de la variable expliquée sont notées ici xi,j, et les variables explicatives sont le temps t et p variables particulières qui n’apparaissent pas directement dans la formule et dont les coefficients de régression sont les variations saisonnières sj.
Le critère des moindres carrés consiste à déterminer les paramètres b, a, s1, s2, …, sp de façon à minimiser la somme des carrés des différences ei,j = xi,j – [( b (i-1) p + j + a + sj ] entre la valeur observée xi,j et la valeur estimée par le modèle b [(i-1) p + j ] + a + sj.
Les valeurs obtenues sont des estimations des paramètres théoriques b, a, sj. Le coefficient de corrélation du modèle est le coefficient de corrélation entre les valeurs observées xi,j et les valeurs estimées xi,j’.
On calculera les estimations des paramètres à l’aide des formules suivantes :
|
a |
= |
m – b ( n p + 1)/2 |
|||
|
sj |
= |
m.j – m – b [ j – ( p + 1 )/2 ] |
|
|||
avec les notations suivantes :
m : moyenne de la totalité des observations
mi. : moyenne des observations de la ligne i
m.j : moyenne des observations de la colonne j
définition : les termes ei,j = xi,j – [ [ b (i-1) p + j ] + a + sj ] sont appelés résidus.
Comme en régression, la variance des résidus s2 dépend du coefficient de corrélation r et de la variance sx2 des observations xi,j de la variable expliquée :
|
s2 = sx2
( 1 – r2) |
L’interprétation du coefficient de corrélation est délicate dans le cas des séries chronologiques. Il est souvent très élevé (une valeur de 0.98 n’est pas rare) sans que l’on puisse en déduire directement que l’ajustement obtenu est satisfaisant. Cette particularité est due au fait que la variable temps est ordonnée. Dès lors, il suffit que la tendance soit croissante ou décroissante pour que le coefficient de corrélation soit élevée. Mais il ne donne aucun renseignement sur la nature de la tendance, qui peut être exponentielle ou linéaire etc.
Exemple : le modèle additif et l'hypothèse de linéarité de la tendance de la série 1 sont confirmés par la représentation graphique (figure 8.8).
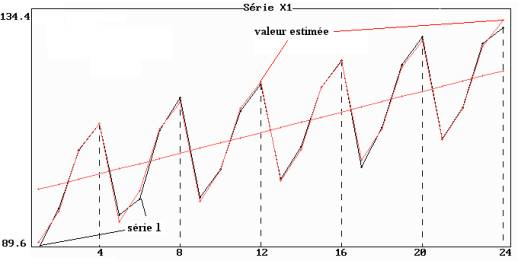
Figure 8.8 : représentation simultanée de la série 1, de la tendance
et des valeurs estimées par le modèle
Nous donnons les résultats partiels suivants :
|
années |
moyennes annuelles mi. |
produits i mi. |
|
1 |
102.57846 |
102.57846 |
|
2 |
106.88766 |
213.77531 |
|
3 |
110.81528 |
332.44585 |
|
4 |
115.15820 |
460.63280 |
|
5 |
118.96325 |
594.81625 |
|
6 |
122.77737 |
736.66425 |
On en
déduit le modèle estimé par le filtre de Buys-Ballot :
|
b =
1.011173 |
a = 100.2237 |
|
s1
= -10.43134 |
s2 = -5.27912 |
|
s3 = 5.77288 |
s4 = 9.93759 |
|
r = 0.99791 |
s² = 0.5641465 |
Tableau 9.8 : paramètres du modèle linéaire additif
estimés par le filtre de Buys-Ballot sur la série 1
L'ajustement peut être considéré comme très précis puisque le coefficient de corrélation entre les observations xi,j et les estimations xi,j' est égal à 0.99791.
La série 1 n'est pas une série réelle : elle a été obtenue par simulation du modèle linéaire additif avec comme paramètres théoriques :
xt = b t + a + st + et
b = 1, a = 100, et » N(0,1), s1 = -10, s2 = -5, s3 = 5, s4 = 10.
Les valeurs estimées sont visiblement très proches des valeurs théoriques. La méthode statistique permet donc de retrouver à partir des observations les valeurs des paramètres utilisés pour générer les données. C’est le moins qu’on pouvait en attendre.
3.2 Validation du modèle linéaire et prévision.
Pour effectuer la prévision xi,jp de la série chronologique à l’instant t = (i-1) p + j, on remplace dans le modèle théorique les paramètres par leurs estimations :
|
xi,jp = b [(i-1) p + j ] + a + sj |
Ces prévisions ponctuelles peuvent être complétées par des prévisions par intervalle de confiance, comme en régression, mais nous ne donnerons pas les formules trop complexes pour être utilisées facilement.
Exemple :
Les valeurs estimées par le modèle sont données par la formule :
|
xi,j = 1.011173 [ (i-1)
4 + j ] + 100.2237 + sj |
avec :
|
s1 = -10.43134 |
s2 = -5.27912 |
s3 = 5.77288 |
s4 = 9.93759 |
Les prévisions concernant l'année 7 sont les suivantes :
|
x7,1p = 115.07169 |
x7,2p = 121.23509 |
x7,3p = 133.29826 |
x7,4p = 138.47414 |
Les prévisions que l'on peut effectuer après l'estimation des paramètres ne sont justifiées que dans la mesure où les hypothèses du modèles sont respectées.
Une hypothèse fondamentale pour la prévision et souvent négligée est que les conditions dans lesquelles la série chronologique évolue sont les mêmes à la date de la prévision que dans le passé. Il faut noter que cette condition n’est pas toujours vérifiée, par l’effet de la prévision elle-même : par exemple, un hypermarché qui prévoit une baisse de son chiffre d’affaires va prendre des mesures de réduction de coût, augmenter sa publicité etc., de façon à augmenter ses ventes : les décisions vont donc à l’encontre de la prévision.
Il est indispensable en outre de contrôler statistiquement le modèle. Pour cela, on étudie les résidus ei,j. Ces résidus possèdent les propriétés mathématiques habituelles en régression : ils sont centrés, indépendants de la variable explicative (ici le temps). Les résidus de chaque trimestre sont en outre de moyenne nulle.
Pour que le modèle soit valide, leur répartition doit être proche de la loi normale. Ils ne doivent présenter pas d'évolution particulière dans le temps, ce que l’on peut vérifier par une représentation graphique ou par des tests (tests de Durbin et Watson, sur le coefficient d’autocorrélation de rang 1).
Rappelons enfin que la prévision xi,jp est la prévision de la moyenne des observations pour t fixé : l’intervalle de confiance donné par certains logiciels est celui de cette moyenne, et non de la valeur individuelle à l’instant t.