4. étude des résidus.

Une régression complète ne se limite pas au calcul des estimations : il est indispensable de valider le modèle estimé, c’est-à-dire de vérifier son adéquation aux données analysées. Pour cela, on utilise les résidus.

4.1 Résidus.

La droite de régression théorique a pour équation :

y = b x + a

Les coefficients de régression théoriques b et a sont évidemment inconnus, et on ne dispose que des estimations b et a de ces coefficients.

À chaque valeur x(i) on peut associer l’estimation b x(i) + a de Y donnée par la droite de régression, et la comparer à la valeur observée y(i) : on obtient ainsi le résidu e(i), qui est l’écart entre la valeur observée y(i) et la valeur b x(i) + a estimée par la régression.

Définition : on appelle résidus les erreurs observées e(i) définies par :

e(i) = y(i) – [ b x(i) + a ]

Les résidus sont des approximations des erreurs inconnues e(i) :

e(i) = y(i) – [ b x(i) + a ].

On montre qu’ils sont centrés (de moyenne nulle) et que leur covariance, donc leur coefficient de corrélation, avec la variable explicative est nulle :

		1	n
me	=	–––	S	e(i)		=	0
		n	i = 1
		1	n
cov (e,x)	=	–––	S	e(i)	[x(i) – mx]	=	0
		n	i = 1

Leur variance est égale à la moyenne de leurs carrés puisque leur moyenne est nulle :

		1	n			1	n
se^2	=	––––	S	(e(i) – me )^2	=	––––	S	e(i)^2
		n	i = 1			n	i = 1

La variance étant un ordre de grandeur des carrés des résidus, l’écart type s_e donne donc un ordre de grandeur des résidus.

La variance s_e², que nous noterons simplement s² conformément à l’usage, s’exprime en fonction du coefficient de corrélation par la formule suivante :

s² = (1 – r² ) s_y²

Exemple : Calculons quelques résidus dans la régression du revenu par l’âge :

x1 = 51 ans,	y1 = 195 888 F,	b x1 + a = 145 645.4 F :	e1 = 50242.6 F
x26 = 45 ans,	y26 = 107808 F,	b x26 + a = 128389.7 F :	e26 = -20 581.7 F

Le coefficient de corrélation est égal à 0.6728 et son carré à 0.4527. On en déduit la variance des résidus :

s² = (1 – 0.4527) = 0.5473 x 874 467 804.91 = 478 596 229.62

L’écart type des résidus (s = 21 876F) est nettement plus petit que celui des revenus (s_y = 29 571.4F). L’âge apporte donc une information importante sur la dispersion des revenus observés.

4.2 Propriétés des résidus.

Le modèle théorique n’est satisfaisant que si les résidus possèdent un certain nombre de propriétés :

· Les résidus et la variable explicative doivent être indépendants. Ce second point peut aussi être contrôlé graphiquement : on représente graphiquement les couples [x(i), e(i)] ou, ce qui revient au même, les couples [b x(i) + a, e(i)] pour détecter une liaison éventuelle entre les deux variables [x(i)] et [e(i)]. Rappelons que cette liaison ne peut être linéaire puisque le coefficient de corrélation entre les résidus et la variable explicative est nul : on pourra trouver par exemple un nuage de points en forme de parabole, dont nous donnons un exemple dans le chapitre 3. La vérification de cette hypothèse est indispensable dans le cas d’observations échelonnées dans le temps (cf. chapitre 8).

· On connaît la propriété suivante fondamentale :

s² = (1 – r² ) s_y²

Pour apprécier la qualité de l’ajustement linéaire, on peut donc utiliser le coefficient de corrélation entre les séries [x(i)] et [y(i)] : un coefficient de corrélation dont le carré est proche de 1 indique des résidus relativement petits par rapport à la variable expliquée. Rappelons que cela ne suffit pas à justifier le modèle linéaire.

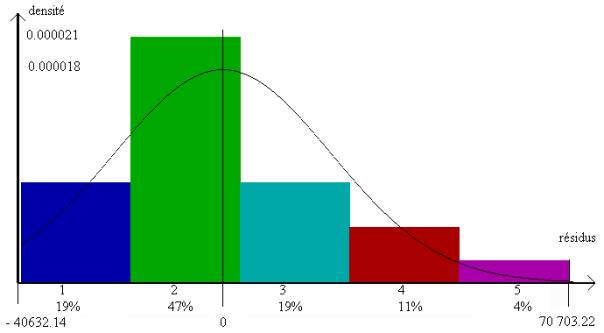
On peut contrôler que la variable résiduelle e suit la loi normale en effectuant un test d’ajustement du c² sur les résidus, bien qu’ici ce test ne soit pas très bien adapté (les procédures correctes sont assez compliquées). La répartition des résidus suivant la règle de classification expliquée dans le chapitre 2 doit donner approximativement les pourcentages correspondant à la loi normale. Cette propriété est surtout utile pour estimer les coefficients de régression et effectuer des prévisions à l’aide d’intervalles de confiance.

Exemple : dans la régression du revenu par l’âge (après élimination des clients de rang 25, 31 et 43), l’histogramme des résidus donné ci-dessous en figure 4 montre une certaine asymétrie de leur répartition. La courbe superposée représente la densité de la loi normale de même moyenne et de même variance ; la proximité ne semble pas très bonne, mais il y a peu de résidus dont la valeur absolue soit particulièrement grande.

Histogramme des résidus (régression du revenu par l’âge)

cinq classes de même amplitude

Pour effectuer le test d’ajustement du c² nous avons regroupé les deux derniers intervalles de façon à assurer la convergence de la loi de la statistique X² vers la loi du c². Le degré de liberté est donc égal à n = k – l – 1 = 2, puisque seule la variance est estimée à partir des données ( k = 4, l = 1).

On trouve :

x^2 = 3.911

ddl: ν = 2

P(X^2>3.911) = 0.13899

On peut donc considérer que la répartition des résidus est gaussienne (notons que si l’on choisit un degré de liberté égal à k – 1 au lieu de k – l – 1 comme nous l’avons proposé dans le chapitre 7, la probabilité critique est égale à 0.27 : la décision est la même).

La représentation des couples [e(i), x(i)] (figure 5), ne montre pas de liaison particulière entre les résidus et la variable explicative (les u.s. ont été renumérotées de 1 à 47) :

Figure 5.7 : représentation graphique des couples (âges, résidus)

(47 couples)

En conclusion, le modèle de régression linéaire donne des résultats relativement satisfaisants.