2. Estimateur d’un paramètre

L’estimation statistique est un chapitre fondamental de la statistique mathématique. Son objectif est d’affecter aux paramètres théoriques des lois de probabilité des valeurs numériques, ou estimations, vérifiant des propriétés précises. Ces valeurs numériques sont les observations de variables aléatoires appelées estimateurs.

2.1 Estimations empiriques.

Considérons tout d’abord la v.a. discrète X définie par la face obtenue en lançant le dé. En relançant le dé 100 fois puis 1000 fois, nous avons obtenu les répartitions suivantes :

Faces	1	2	3	4	5	6
Probabilités	1/6	1/6	1/6	1/6	1/6	1/6
Proportions (100 valeurs)	0.16	0.12	0.16	0.14	0.21	0.21
Proportions (1000 valeurs)	0.175	0.162	0.154	0.164	0.162	0.183

Tableau 2.5 : résultats des lancers d’un dé équilibré à 6 faces

Les moyennes sont donc :

Moyenne théorique :

m	= p₁ x x₁	+ p₂ x x₂	+ p₃ x x₃	+ p₄ x x₄	+p₅ x x₅	+ p₆ x x₆
	= (1/6) x 1	+ (1/6) x 2	+ (1/6) x 3	+ (1/6) x 4	+ (1/6) x 5	+ (1/6) x 6

Moyenne observée

= f₁ x x₁

+ f₂ x x₂

+ f₃ x x₃

+ f₄ x x₄

+ f₅ x x₅

+ f₆ x x₆

sur les 100 valeurs :

m₁₀₀

= 0.16 x 1

+ 0.12 x 2

+ 0.16 x 3

+ 0.14 x 4

+ 0.21 x 5

+ 0.21 x 6

sur les 1000 valeurs :

m₁₀₀₀

= 0.175 x 1

+ 0.162 x 2

+ 0.154 x 3

+ 0.164 x 4

+ 0.162 x 5

+ 0.183 x 6

On trouve :

m = 3.5

m₁₀₀= 3.75

m₁₀₀₀= 3.525

La proximité entre la moyenne théorique (3.5) et les moyennes observées (3.75 et 3.525) est due à la convergence des proportions observées f_i vers les probabilités p_i. Plus les effectifs sont importants, plus ces proportions sont proches des probabilités, et plus la moyenne observée est proche de la moyenne théorique (au sens de la convergence en probabilité).

Il y a également convergence dans le cas d’une v.a. continue. Examinons le cas de la loi uniforme que nous avons simulée dans le paragraphe précédent (figure 3.5).

Toutes les valeurs observées appartenant à la première classe sont proches du centre de cette classe, soit 0.1. De même pour les autres classes.

Classe	[0, 0.2 [	[0.2, 0.4 [	[0.4, 0.6 [	[0.6, 0.8 [	[0.8, 1 [
Centre	0.1	0.3	0.5	0.7	0.9
Proportion	0.23	0.19	0.15	0.22	0.21

Tableau 3.5 : Classification des 100 observations d’une v.a. de loi uniforme sur ]0, 1[

Une valeur approximative de la moyenne est donc donnée par :

m =

0.23 x 0.1

+ 0.19 x 0.3

+0.15 x 0.5

+0.22 x 0.7

+0.21 x 0.9

= 0.498

La moyenne observée m (= 0.498) est très proche de la moyenne théorique m (= 0.5). Cette proximité est d’autant plus forte que les nombres d’observations et de d’intervalles augmentent, puisque, comme nous l’avons vu sur la figure 4.5 :

· la proportion dans chaque intervalle converge vers la probabilité théorique ;

· les longueurs des intervalles tendent vers 0 et les valeurs sont de plus en plus proches du centre de la classe à laquelle elles appartiennent. .

La limite de la moyenne observée dans ces conditions est par définition l’intégrale de la fonction x f(x) : on retrouve la moyenne d’une v.a. continue.

Le calcul détaillé que nous avons effectué pour montrer la convergence de la moyenne empirique vers la moyenne théorique peut être appliquée au cas de la variance :

· Variance théorique :

s²

= p₁ x x₁²

+ p₂ x x₂²

+ p₃ x x₃²

+ p₄ x x₄²

+ p₅ x x₅²

+ p₆ x x₆² - m²

· Variance observée :

s²

=f₁ x x₁²

+ f₂ x x₂²

+ f₃ x x₃²

+ f₄ x x₄²

+ f₅ x x₅²

+ f₆ x x₆² – m²

On trouve, en notant s₁₀₀² et s₁₀₀₀² les variances des échantillons de taille 100 et 1000 :

s² = 2.917

s₁₀₀²= 3.0008

s₁₀₀₀² = 3.045

Les convergences des proportions f_i vers les probabilités p_i et de la moyenne empirique m vers la moyenne théorique m assurent celle de la variance empirique vers la variance théorique. Mais cette convergence en probabilité est soumise au hasard, et c’est pour cela que la variance empirique s₁₀₀² précédente est plus proche de la variance théorique s² que s₁₀₀₀².

Naturellement, les v.a. continues vérifient la même propriété.

Définition :

· On appelle estimation empirique de la moyenne d’une variable aléatoire la moyenne calculée sur les observations effectuées.

· On appelle estimation empirique de la variance d’une variable aléatoire la variance calculée sur les observations effectuées.

Propriété :

Les estimations empiriques de la moyenne et de la variance convergent en probabilité vers les paramètres théoriques lorsque le nombre d’observations augmente indéfiniment.

2.2 Estimateurs de la moyenne et de la variance.

On peut formaliser la notion d’échantillon et d’estimation. En effet, une suite d’observations x_i d’une v.a. X peut être considérée comme une suite d’observations de n variables aléatoires X_i suivant la loi de X, correspondant chacune à un tirage au hasard dans la population. Il existe donc deux notions d’échantillons :

Définitions :

· L’échantillon de v.a. X_i, i = 1, …, n, est une suite de v.a. indépendantes et de même loi que X, la v.a. X_i représentant simplement la v.a. X au i^ième tirage.

· L’échantillon observé x_i, i = 1, …, n, est une suite de valeurs observées de la v.a. X ou de chaque v.a. X_i, i = 1, …, n.

Définition : on appelle estimateur d’un paramètre d’une loi de probabilité d’une v.a. X une v.a. calculée sur un échantillon X_i, i = 1, …, n de X, dont la valeur observée est une approximation de ce paramètre, et qui vérifie certaines propriétés d’optimalité.

Les estimateurs les plus utilisés sont les estimateurs empiriques de la moyenne et de la variance.

La moyenne observée de la suite x_i, i = 1, …, n est par définition le nombre m :

	1	n
m =	–––	S	x_i
	n	i = 1

La moyenne de l’échantillon X_i, i = 1, …, n, est par définition la v.a. M :

	1	n
M =	–––	S	X_i
	n	i = 1

En conclusion, M est une v.a. dont la valeur observée à l’issue d’une suite de n tirages au hasard est égale à m : la v.a. M est antérieure aux tirages, et m en est une valeur observée, postérieure aux tirages.

On peut définir de la même façon l’estimateur de la variance :

	1	n
V =	–––	S	(X_i – m)²
	n	i = 1

dont la valeur observée v est la variance de l’échantillon observé :

	1	n
v =	–––	S	(x_i – m)²
	n	i = 1

On ne peut toutefois calculer cet estimateur que si l’on connaît la moyenne théorique m, ce qui n’est pas le cas en général. On considère donc souvent l’estimateur ci-dessous :

	1	n
S² =	–––	S	(X_i – M)²
	n	i = 1

dont la valeur observée s² est la variance de l’échantillon observé :

	1	n
s² =	–––	S	(x_i – m)²
	n	i = 1

Définitions :

· L’estimateur empirique de la moyenne théorique d’une v.a. est la v.a. M :

	1	n
M =	–––	S	X_i
	n	i = 1

· L’estimateur empirique de la variance théorique est la v.a. S² :

	1	n
S² =	–––	S	(X_i – M)²
	n	i = 1

2.3 Propriétés caractéristiques des estimateurs.

Ce que l’on appelle estimation en statistique inférentielle regroupe des méthodes beaucoup plus générales que celles que nous avons présentées dans les paragraphes précédents. Les estimateurs empiriques comme M et S² ne sont pas toujours les « meilleurs » pour estimer la moyenne et la variance théoriques d’une loi de probabilité. Dans le cas d’une v.a. qui suit la loi de Poisson P(l) par exemple, le paramètre l est à la fois la moyenne et la variance de la v.a. : l’estimateur de l qu’il faut choisir est-il M ou S² ?

Pour répondre à ce genre de question, il est nécessaire de formaliser la démarche et de préciser ce que l’on entend par « meilleur ». On cherche donc des estimateurs possédant certaines propriétés. En voici quelques-unes :

Un estimateur d’un paramètre w est :

· sans biais si son espérance est égale à w, et biaisé dans le cas contraire ;

· asymptotiquement sans biais si son espérance converge vers w lorsque le nombre d’observations tend vers l’infini ;

· convergent si sa valeur observée converge en probabilité vers w lorsque le nombre d’observations tend vers l’infini ;

· efficace s’il n’existe pas d’estimateur sans biais de w de variance strictement inférieure.

Les estimateurs empiriques précédents possèdent des propriétés particulières :

· L’estimateur empirique de la moyenne est sans biais.

· L’estimateur empirique de la variance est asymptotiquement sans biais.

· Ils sont convergents.

· Lorsque les v.a. X_i suivent la loi normale, l’estimateur empirique de la moyenne est efficace.

En ce qui concerne le second des quatre points précédents, on montre que l’estimateur empirique de la variance a pour espérance (n-1) s²/n. Cela explique que, surtout pour des échantillons de taille faible, on choisit souvent comme estimateur ponctuel de s² la statistique S’² = n S²/(n-1). On a en effet (ex. 3) :

E(S’²) = E[ n S²/(n-1) ] = n E(S²) /(n - 1) = s²

2.4 Loi de l’estimateur de la moyenne (théorème de la limite centrée).

Théorème de la limite centrée : on considère une suite de n v.a. X_i indépendantes et de même loi de probabilité, d’espérance m et de variance s². La loi de probabilité de l’estimateur M est, pour une valeur suffisante de n, la loi normale d’espérance m et de variance s²/n.

L’expression « valeur suffisante de n » est vague : cela vient du fait que le nombre n à partir duquel on peut considérer que la loi de M est normale dépend de la loi des v.a. X_i.

Par exemple, si les v.a. X_i suivent elles-mêmes la loi normale, il suffit que n soit supérieur ou égal à 1 : la propriété est toujours vraie. Pour une loi uniforme, on considère en général n = 12, ou n = 24. Dans le cas de lois non symétriques comme la loi exponentielle, la valeur minimale de la taille de l’échantillon assurant la convergence vers la loi normale peut être beaucoup plus grande (>50).

Étudions le cas de v.a. X_i suivant la loi uniforme sur ] 0, 1 [. La moyenne théorique est égale à m = 0.5 et la variance à s²= 1/12. Un échantillon de cette loi, pour une taille suffisante, n = 24 par exemple, aura pour moyenne une valeur m proche de 0.5 et pour variance une valeur s² proche de 1/12. Ces valeurs m et s² sont les valeurs observées des estimateurs M et S² :

0.628	0.923	0.935	0.397	0.955	0.133	0.978	0.491
0.247	0.781	0.715	0.493	0.853	0.379	0.914	0.161
0.308	0.891	0.003	0.271	0.094	0.427	0.962	0.946

Tableau 4.5 : 24 observations de la loi uniforme sur ] 0, 1 [

m = 0.5785487, s² = 0.1043021

Le théorème de la limite centrée dit que la variable M suit la loi normale de moyenne m et de variance s²/n. La simulation par ordinateur concrétise cette propriété : en générant 100 échantillons de taille 24, on obtient 100 valeurs observées m₁, m₂, …, m₁₀₀ de M.

On constate effectivement, sur la figure 5.5, la proximité de l’histogramme de ces 100 valeurs avec la densité théorique de la loi normale.

On pourra, en simulant des échantillons de taille 12 d’une v.a. suivant la loi exponentielle par le logiciel TESTEAO[1], constater que la taille de ces échantillons est très insuffisante pour que leur moyenne suive la loi normale.

Ce théorème est vrai aussi lorsque la v.a. est discrète, avec les mêmes réserves sur la taille n de l’échantillon nécessaire pour que la convergence de la v.a. M vers la loi normale soit acceptable.

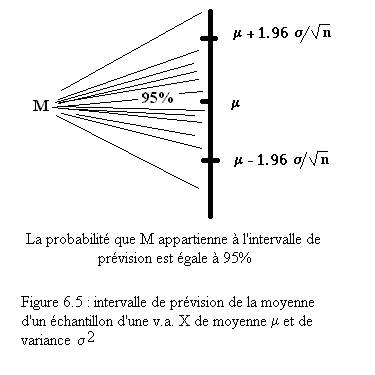
Une première application est de permettre une prévision de la valeur moyenne observée si l’on connaît les paramètres théoriques de la loi de probabilité des X_i.

Exemple : on lance 100 fois le dé. D’après le théorème de la limite centrée, la moyenne empirique M définie par la moyenne des 100 chiffres obtenus suit approximativement la loi normale d’espérance m = 3.5 et de variance s²/n = 0.0292. On peut donc effectuer des calculs de probabilités sur cette v.a. :

· La probabilité de l’intervalle [m - 1.96 s /Ön, m + 1.96 s /Ön] = [3.165, 3.835] est égale à 0.95. Il est donc très probable que la valeur moyenne obtenue en lançant le dé 100 fois soit comprise entre ces deux valeurs.

· La probabilité de l’intervalle ]-¥ , m - 1.6449 s /Ön] = ]-¥ , 3.219 ] est égale à 0.05. On est presque sûr d’obtenir une valeur moyenne supérieure à 3.219.

2.5 Loi de l’estimateur de la variance.

L’étude de l’estimateur de la variance est fondée sur une propriété supplémentaire : la loi des v.a. X_i doit être la loi normale.

Théorème : si les v.a. X_i , i = 1, …, n sont indépendantes et suivent la loi normale d’espérance m et de variance s², la v.a. n S²/s² suit la loi du c² de degré de liberté n - 1.

Ce théorème est une conséquence de la définition de la loi du c². La v.a. n S²/s² est une somme de carrés de variables qui suivent approximativement la loi normale centrée réduite, si les X_i suivent la loi normale :

n S²		(X₁ – M)²		(X₂ – M)²		(X₃ – M)²	^…		(X_n – M)²
–––	=	–––––––	+	––––––––	+	––––––––		+	––––––––
s²		s²		s²		s²	…		s²

Le degré de liberté est diminué de 1 pour tenir compte du fait que les variables de la forme (X_i – M) / s, ne sont pas indépendantes puisqu’elles dépendent toutes de M, et qu’elles ne sont pas exactement de variance 1. On notera que la connaissance de la moyenne théorique m n’est pas nécessaire pour appliquer le théorème.

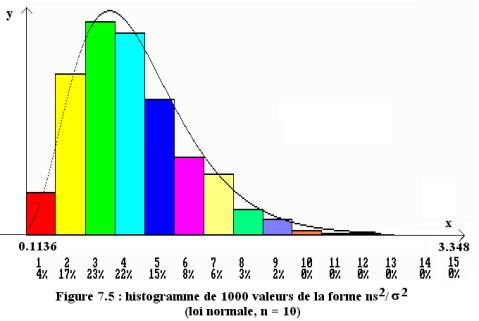
Nous avons simulé, pour visualiser la loi de probabilité de la v.a. n S²/s², 1000 échantillons de taille n de la loi des X_i, construit l’histogramme des valeurs n s²/s² obtenues, et superposé la loi du c² correspondante.

En figure 7.5, la loi des v.a. X_i simulée est la loi normale et chaque échantillon de taille 10. On constate la proximité entre l’échantillon et la loi du c², ce qui confirme le théorème.

L’histogramme est par contre différent de la densité de la loi du c² lorsque ces variables suivent la loi uniforme (figure 8.5).

Comme dans le cas de l’estimateur M, on peut prévoir dans quel intervalle se trouvera probablement la variance calculée sur n observations d’une v.a. qui suit la loi normale de moyenne m et de variance s².

Exemple : supposons n = 50 et s² = 25. La v.a. X² = 50 S²/25 = 2 S² suit la loi du c² de degré de liberté 49 (on suppose donc que les v.a. X_i suivent la loi normale). La table statistique pour n = 49 degrés de liberté donne les valeurs suivantes :

P(2 S²< 31.55) = 0.025

P(2 S²> 70.22) = 0.025

On en déduit la probabilité ci-dessous :

P(31.55 <2S²<70.22) = 0.95

La variance de l’échantillon sera très probablement comprise entre 15.78 et 35.36 :

P(15.78 < S²< 35.36) = 0.95

[1] Introduction aux tests statistiques, Enseignement Assisté par Ordinateur, de T. Foucart, Technip, Paris, 1991.