1. Probabilités. probabilités conditionnelles.
1.1 Population et événements.
Les définitions données ci-dessous établissent en fait une équivalence entre le langage des probabilités et le langage de la théorie des ensembles. Nous utiliserons dans la suite ces deux langages suivant le contexte.
· On appelle population statistique un ensemble W constitué de N éléments appelés unités statistiques (notées u.s.) ou individus. Le nombre N est appelé nombre de cas possibles.
· On appelle événement un sous-ensemble de la population W. Le nombre NA d’u.s. appartenant à un événement A est appelé « nombre de cas favorables ».
Cette population est celle dans laquelle on effectuera ultérieurement des tirages au hasard, et nous serons parfois amenés à la considérer comme infinie, de même que le nombre d’u.s. appartenant à un événement. Elle est souvent appelée urne en probabilités.
Nous dirons que l’événement A s’est réalisé si l’unité statistique tirée au hasard appartient au sous-ensemble A.
On considère deux sous-ensembles A et B de W.
· Il existe deux événements très particuliers :
§ L’événement certain caractérisé par la population W.
§ L’événement impossible ou ensemble vide noté par la lettre grecque F (phi).
· On dit que B est inclus dans A si tous les éléments de B appartiennent à A (figure 1).

L’inclusion signifie en particulier que si B est inclus dans A, la réalisation de l’événement B, définie par le tirage d’un élément de B, entraîne la réalisation de l’événement A puisque l’élément tiré, s’il appartient à B, appartient aussi à A.
Réciproquement, si la réalisation de B entraîne toujours celle de A, tout élément de B appartient à A et le sous-ensemble B est inclus dans le sous-ensemble A.
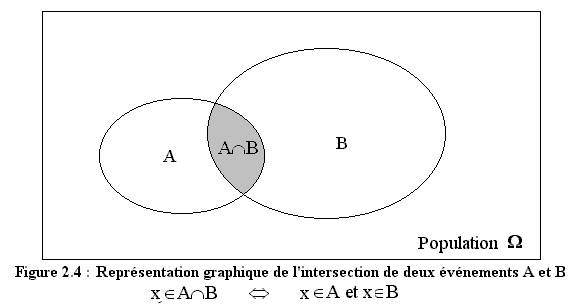
· L’ensemble « A inter B » ou événement « A et B » noté AÇB, est constitué des éléments qui appartiennent à la fois à A et à B.
· L’ensemble « A union B » ou événement « A ou B » noté AÈB est constitué des éléments de A, de B ou de A et B (figure 2). On dit que le « ou » est inclusif.

On a donc la relation suivante : [AÇB] Ì [AÈB].
· le sous-ensemble complémentaire d’un sous-ensemble B (figure 4) est défini par le sous-ensemble A tel que :
|
AÈB = W |
AÇB = F. |

On note
alors : A
= Bc
Le complémentaire de A = Bc est évidemment Ac = B. La population W et l’ensemble vide F sont complémentaires.
1.2 Définition et propriétés des probabilités.
On considère une population W d’effectif N et un événement A d’effectif NA.
Définition : on appelle probabilité de l’événement A le rapport NA/N.
La probabilité NA/N est égale à ce que l’on appelle couramment « le rapport du nombre de cas favorables NA au nombre de cas possibles N ».
Cette notion de probabilité est appelée équiprobabilité : la probabilité d’un événement constitué d’une seule unité statistique est constante et égale à 1/N.
Définition : Tirages avec et sans remise :
· L’unité statistique tirée peut être remise dans la population et être éventuellement retirée : le tirage est dit indépendant puisqu’il n’exerce aucune influence sur les tirages suivants.
· Inversement, si l’u .s. n’est pas remise, les nombres NA et N sont diminués de 1 : après le premier tirage, la probabilité de l’événement A devient (NA – 1)/(N – 1) et n’est plus la même : les tirages sont « dépendants » ou « sans remise ».
· La probabilité est un nombre compris entre 0 et 1 :
0 £ P(A) £ 1
Cette propriété est évidente, le nombre de cas favorables étant toujours positif ou nul et inférieur ou égal au nombre de cas possibles.
· La probabilité de la population W est égale à 1 et celle de l’ensemble vide F à 0 :
|
P(W) = 1 |
P(F) = 0 |
Lorsque l’événement est la population W, les cas favorables sont les cas possibles : il y a égalité des effectifs, et lorsque c’est l’ensemble vide F, le nombre de cas favorables est nul.
· La probabilité de l’événement complémentaire est égale à :
|
P(Ac) = 1 – P(A) |
Les éléments de Ac sont ceux qui n’appartiennent pas à A. Il y en a donc N – NA, d’où la relation.
· La probabilité de l’union de deux événements est donnée par :
|
P(AÈB) = P(A) + P(B) – P(AÇB) |
Les éléments de A È B sont les éléments de A (il y en a NA), les éléments de B (il y en a NB). En ajoutant NA et NB, on compte deux fois les éléments qui appartiennent à la fois à A et à B, c’est-à-dire de AÇB : il est donc nécessaire de les soustraire une fois. D’où la relation précédente dite « additivité forte ».
· Si un sous-ensemble B est inclus dans un sous-ensemble A, la probabilité P(B) est inférieure ou égale à la probabilité P(A)
|
B Ì A |
Þ |
P(B) £ P(A) |
C’est une conséquence directe de la définition de l’inclusion : tous les éléments de B appartiennent à A : le nombre d’éléments de B est inférieur ou égal au nombre d’éléments de A et par suite le rapport NB/N est inférieur au rapport NA/N.
Définition généralisée d’une probabilité et d’un espace
probabilisé :
Il n’est pas toujours possible de définir la population, les événements et les probabilités comme précédemment, en particulier dans le cas où la population est infinie, comme par exemple un ensemble de nombres. Pourtant, il est naturel de considérer que si l’on tire au hasard un nombre entier, il y a une chance sur deux d’obtenir un nombre pair, une chance sur trois un nombre divisible par trois … On est donc amené à généraliser les définitions précédentes de la façon suivante :
· un univers est un ensemble quelconque W.
· les événements sont des sous-ensembles de W tels que l’union d’événements, l’intersection et la complémentation sont des événements.
· la probabilité est une application qui à tout événement A associe un nombre P(A) vérifiant les propriétés précédentes.
La formalisation de la population considérée est parfois complexe. Elle est rarement indispensable, et souvent il n’est pas indispensable d’en donner la définition précise. Dans toute la suite du chapitre, les propriétés seront explicitées dans le cas de la définition initiale de la probabilité (rapport du nombre de cas favorables au nombre de cas possibles).
1.3 Indépendance et probabilité conditionnelle.
La formule de Bayes (18e siècle) permet de prendre en compte la réalisation d’un événement pour réévaluer la probabilité d’un autre. Par exemple, la réalisation de l’événement A : « la personne est de sexe féminin » a un impact évident sur la probabilité de l’événement B : « la personne chausse du 41», peu de femmes chaussant du 41.
Considérons deux événements A et B, d’effectifs NA et NB. On note NAÇB l’effectif du sous-ensemble AÇB. Dans l’exemple précédent, AÇB est l’ensemble de femmes chaussant du 41 et NAÇB leur nombre.
Supposons que l’événement A soit
réalisé : on a donc tiré un élément parmi les NA éléments de A.
Examinons ensuite la probabilité de B : elle est maintenant définie par le
rapport NAÇB/NA :
|
NAÇB |
|
NAÇB |
|
NA |
|
________ |
= |
_______ |
/ |
____ |
|
NA |
|
N |
|
N |
Définition : La probabilité conditionnelle d’un événement B pour un événement A fixé de probabilité non nulle est définie de la façon suivante :
P(B/A) = P(BÇA)/P(A)
La probabilité de B n’a pas changé si l’on a :
|
NAÇB |
|
NB |
|
_______ |
= |
____ |
|
NA |
|
N |
Cette relation peut s’écrire de la façon suivante :
|
NAÇB |
|
NA |
|
NB |
|
________ |
= |
_____ |
x |
_____ |
|
N |
|
N |
|
N |
Définition : on dit que deux événements A et B sont indépendants quand la réalisation de l’un ne modifie pas la probabilité de l’autre.
Propriété caractéristique : deux événements A et B sont indépendants si et seulement si la probabilité de l’événement A Ç B est égale au produit des probabilités :
Exemple : on lance un dé à 6 faces. On étudie les événements A : le chiffre obtenu est pair, B : le chiffre obtenu est inférieur ou égal à 3, C : le chiffre obtenu est 1, 3, 4 ou 6.
On a : P(A) = 1/2 P(B)
= 1/2 P(C) = 2/3
A Ç B: le chiffre obtenu est pair et compris entre 1 et 3, donc c’est 2 : P(A Ç B) = 1/6.
P(A) P(B) = 1/4 : A et B ne sont pas indépendants.
A Ç C : le chiffre obtenu est 4 ou 6 : P(A Ç C) = 2/6
P(A) P(C) = 2/6 : A et C sont indépendants.
Calculons les probabilités conditionnelles :
P(B/A) = P(A Ç B)/P(A) = (1/6 ) / (1/2) = 1/3¹ P(B) = 1/2
P(C/A) = P(A Ç C)/P(A) = (2/6 ) / (1/2) = 2/3=
P(C) = 2/3
Formule de Bayes : soit A un événement de W. On considère un événement B et son
complémentaire Bc . On
a :
|
|
|
P(A/B) P(B) |
|
P(B/A) |
= |
___________________________________ |
|
|
|
P(A/B)
P(B) + P(A/Bc) P(Bc) |
La démonstration de cette formule est donnée dans les compléments.
Exemple : il y a une femme sur deux adultes dans la population française, et, parmi les femmes, une sur dix chausse du 41, la proportion étant de un sur cinq chez les hommes. Calculons la probabilité qu’une personne chaussant du 41 soit une femme.
On note A l’événement « la personne chausse du 41 », B l’événement « la personne est une femme » et évidemment Bc l’événement « la personne est un homme ». On a donc :
|
P(B) = 1/2 |
P(Bc) = 1/2 |
|
P(A/B) = 1/10 |
P(A/Bc) = 1/5 |
On en déduit :
|
|
|
(1/10) x (1/2) |
|
1 |
|
P(B/A) |
= |
_________________________________ |
= |
____ |
|
|
|
(1/10) x (1/2) + (1/5) x (1/2) |
|
3 |