3. Propriétés du coefficient de corrélation.

3.1 Propriétés mathématiques du coefficient de corrélation linéaire.

Propriété fondamentale : le coefficient de corrélation linéaire d’une série de couples d’observations (x_i, y_i) i = 1, …, n est compris entre -1 et 1. S’il est égal à ±1, les couples (x_i, y_i) i = 1, …, n vérifient exactement une relation linéaire de la forme :

quel que soit i = 1, …, n

a xi + b yi + c = 0

où a et b sont deux nombres réels constants et les points qui les représentent sont strictement alignés.

En fait, le coefficient de corrélation linéaire possède des propriétés mathématiques fondamentales analogues à celles du cosinus d’un angle.

La propriété fondamentale précédente est connue sous le nom d’inégalité de Schwarz.

3.2 Interprétation du coefficient de corrélation. Liaison linéaire.

L’interprétation du coefficient de corrélation linéaire n’est pas aussi facile qu’on le croit généralement :

· Plus il est proche de 1 ou de ‑1, plus les points sont proches d’une droite. S’il est égal à ± 1, les points sont strictement alignés.

· pour préciser une valeur à partir de laquelle on peut considérer le coefficient comme proche de 1 ou de –1, on utilise une table statistique (paragraphe 3.3).

· on peut obtenir des coefficients de corrélation très proches de 1 (0.95) sur des données non linéaires (par exemple, des données de la forme y = e^x).

· on peut obtenir des coefficients de corrélation nuls sur des données liées par une relation non linéaire exacte (cf. l’exemple donné plus loin).

· une relation statistique, détectée par le coefficient de corrélation ou par un graphique, ne montre jamais de relation causale entre deux variables. La causalité ne peut être déduite que d’une analyse non statistique des données.

Nous donnons ci-dessous trois schémas caractéristiques des valeurs du coefficient de corrélation dans le cas d’une liaison linéaire.

Lorsque le coefficient de corrélation est proche de 1 (il est égal à 0.9 en figure 5.1), les observations dans les quadrants I et III sont beaucoup plus nombreuses dans les quadrants II et IV et presque alignées le long d’une droite appelée axe principal.

Figure 5.1.3 : Coefficient de corrélation proche de 1

En figure 5.2, le coefficient de corrélation est égal à –0.7: les observations sont plus nombreuses dans les quadrants II et IV et sont moins bien alignées. L’axe principal apparaît encore assez nettement.

Figure 5.2.3 : Coefficient de corrélation proche de –1

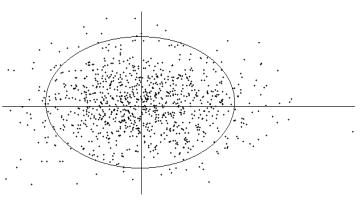
En figure 5.3, les observations sont réparties de façon uniforme dans les quatre quadrants : le coefficient de corrélation est très proche de 0 et l’axe principal n’apparaît plus.

Figure 5.3.3 : Coefficient de corrélation proche de 0

L’axe principal représenté sur les graphiques n’est pas la droite de régression que nous définirons au chapitre 7. Il est déterminé de la façon suivante : c’est la droite telle que la somme des carrés des distances des points à cette droite soit la plus petite possible. Nous retrouverons cette notion dans le chapitre 9.

Exemple : le coefficient de corrélation entre l’âge et le revenu des 50 clients de l’hypermarché est égal à 0.298 sur les données individuelles. La figure 2 montre que les points sont relativement éloignés d’une droite du fait surtout des clients de rangs 25, 31 et 43. Le coefficient de corrélation n’est pas ici un paramètre statistique très fiable.

Une liaison dangereuse : nous donnons ci-dessous une série de 10 couples (x_i, y_i) tels que y_i soit égal à f(x_i) . Le lecteur pourra calculer le coefficient de corrélation r(x,y) et vérifier qu’il est égal à 0. La représentation graphique des couples montre une liaison fonctionnelle évidente qui n’est pas linéaire :

i	xi	yi	i	xi	yi
1	-0.5979	0.8868	6	-2.1125	-1.3455
2	1.5204	-0.1957	7	0.1706	1.0187
3	1.1423	0.3179	8	-1.9535	-0.9815
4	-0.0256	1.0451	9	0.6340	0.7997
5	2.4093	-1.8863	10	-1.1871	0.3409

10 couples liés fonctionnellement

dont le coefficient de corrélation est nul

Ce genre de liaison peut exister en particulier dans les analyses de séries chronologiques (chapitre 8) et multidimensionnelles (chapitre 9).

figure 6.3 : représentation d’un ensemble de couples

(x,y) tels que y= f(x), r(x,y) = 0

3.3 Répartitions normales.

Une autre condition pour que le coefficient de corrélation linéaire soit fiable est que les distributions des séries suivent à peu près la loi normale, c’est-à-dire que les histogrammes ne soient pas très différents de la courbe en cloche (cf. chapitre 1).

Lorsque cette propriété est vérifiée, on connaît la répartition du coefficient de corrélation calculé sur une série de n couples dont le coefficient de corrélation théorique est égal à 0. Nous anticipons ici sur le chapitre 6 pour donner une règle de classement de ce paramètre : un coefficient de corrélation supérieur en valeur absolue à la valeur donnée dans le tableau 2.3 pour le nombre d’observations correspondant montre l’existence d’une liaison réelle entre les variables.

n	valeur limite	n	valeur limite	n	valeur limite
10	0.6319	60	0.2542	150	0.1603
20	0.4438	70	0.2352	160	0.1552
30	0.3610	80	0.2199	170	0.1506
40	0.3120	90	0.2072	180	0.1463
50	0.2787	100	0.1966	200	0.1388

Tableau 2.3 : valeurs limites du coefficients de corrélation

Exemple : On donne ci-dessous l’histogramme des revenus des 50 clients observés d’Euromarket (figure ).

Figure 7.3 : Histogramme des revenus et courbe en cloche

(50 clients,5 intervalles de même amplitude)

Il est très différent de la courbe en cloche : les revenus ne sont pas répartis parmi les 50 clients d’Euromarket suivant la loi normale, et l’interprétation du coefficient de corrélation doit être prudente.

3.4. Matrices de corrélation.

L’analyse de la corrélation est beaucoup plus compliquée dans le cas de plus de deux variables. Dans l’exemple donné, on a observé simultanément l’âge, le revenu, le nombre d’enfants et les dépenses des 50 clients. Il y a donc 4 variables. Les coefficients de corrélation à calculer concernent :

· l’âge et successivement le revenu, le nombre d’enfants, les dépenses (3 coefficients) ;

· le revenu et successivement le nombre d’enfants, les dépenses (2 coefficients) ;

· le nombre d’enfants et les dépenses (1 coefficient).

Donc en tout 6 coefficients de corrélation.

Le même raisonnement nous montrerait que pour 10 variables, on a 45 coefficients de corrélation à calculer et que dans le cas général, pour p variables, le nombre de coefficients de corrélation est égal à p(p – 1) /2. Pour p = 20, cela donne 190 coefficients de corrélation.

Le problème n’est pas dans le calcul, vite résolu par le recours à l’informatique ; il est dans le tracé des graphiques, qui sont aussi nombreux que les coefficients de corrélation, et dans l’interprétation globale des relations entre les variables.

Il existe une méthode spécifique pour analyser ce genre de données : l’analyse en composantes principales, que nous expliquons rapidement dans le chapitre 9.

On présente en général les coefficients de corrélation sous la forme d’un tableau à double entrée, chaque ligne et chaque colonne du tableau correspondant à une variable. Un tel tableau est appelé matrice de corrélation et possède plusieurs propriétés, entre autres :

· La diagonale constituée des termes figurant à la i^e ligne et à la i^e colonne est constituée de 1 ;

· Il est symétrique par rapport à cette diagonale.

Exemple : nous donnons ci-dessous la matrice des corrélations entre l’âge, le revenu, les achats et le nombre d’enfants.

Le coefficient de corrélation entre l’âge et le nombre d’enfants est égal à –0.192. Il serait utile de représenter graphiquement les couples (âge, nombre d’enfants) pour expliquer pourquoi il est négatif. C’est là un des intérêts du coefficient de corrélation : il suscite des interrogations, auxquelles les réponses sont souvent intéressantes.

	âge	revenu	achats	nb. enfants
âge	1.000
revenu	0.298	1.000
achat	-0.132	0.137	1.000
nb. enfants	-0.192	0.384	0.626	1.000