4. Fonction de répartition. quantiles.
L’introduction de la fonction de répartition va nous être utile pour définir les quantiles dont l’utilisation dans les statistiques officielles est très fréquente, ainsi que la notion de concentration bien connue en gestion sous le nom de règle des 80%– 20%.
4.1 Fonction de répartition
Définition : on appelle fonction de répartition d’une série d’observations (xi) i = 1, …n la fonction qui, à un nombre réel quelconque x , associe la proportion d’observations inférieures ou égales à x. On la note en abrégé f.d.r.
Exemple numérique : on considère la série de 6 observations : x1 = 10, x2 = 11, x3 = 12, x4 = 13, x5 = 14, x6 = 15 . La fonction de répartition précédente est constante et égale à 1/6 sur chaque intervalle séparant deux observations successives, par exemple sur l’intervalle [11, 12 [.

Figure 1.2 : Fonction de répartition (6 observations)
La fonction de répartition, notée en général par F(x), est définie pour tout nombre x. Elle possède des propriétés évidentes que l’on constate sur la figure 2 :
· En notant inf(xi) et sup(xi) la plus petite et la plus grande des valeurs observées, on a :
|
Pour tout x < inf (xi) |
F(x) = 0 |
Pour tout x ³ sup(xi) |
F(x) = 1 |
En effet , le nombre d’observations strictement inférieures à la plus petite d’entre elles est nul, et le nombre d’observations inférieures ou égales à la plus grande est égal à n.
· Elle est croissante : x £ x’Þ F(x) £ F(x’). Cela correspond à la propriété suivante (figure 1) : le nombre d’observations inférieures à x = 10 est plus petit que le nombre d’observations inférieures à x’ =12. Cette propriété est vraie dès que x £ x’.
· C’est une fonction « en escalier », c’est– à– dire qu’elle est constante sur des intervalles successifs. .
Il est commode de classer les observations par valeurs croissantes : x(1), x(2), ..., x(n). La valeur x(1) est la plus petite valeur observée, et x(n) la plus grande. Soient x(i) et x(i+1) les observations de rang i et i+1 ( on suppose x(i) < x(i+1) ). Le nombre d’observations inférieures ou égales à x est constant et égal à i quel que soit x appartenant à l’intervalle [x(i), x(i+1) [.
On a ainsi :
|
quel que soit x Î [x(i), x(i+1) [ |
F(x) = i/n |
Dans l’intervalle suivant [x(i+1), x(i+2) [ , on a :
|
quel que soit x Î [x(i+1), x(i+2) [ |
F(x) = ( i + 1 )/n |
La fonction augmente donc par palier de 1/n. Dans le cas ou deux observations sont égales : x(i) = x(i+1), la fonction augmente de 2/n. Dans le cas général, elle augmente d’un multiple de 1/n et reste constante sur chaque intervalle.
La fonction de répartition exacte d’une série d’observations n’est pas difficile à calculer, mais c’est un travail long et fastidieux. On se limite souvent à en calculer la valeur en quelques points, que l’on joint entre eux par un segment de droite (c’est une interpolation linéaire) ou inversement on détermine les points auxquels elle prend une valeur fixée.
Exemple :
nous avons calculé par ordinateur la fonction de répartition des achats des 50
clients d’EUROMARKET. Il s’agit ici d’un calcul exact.
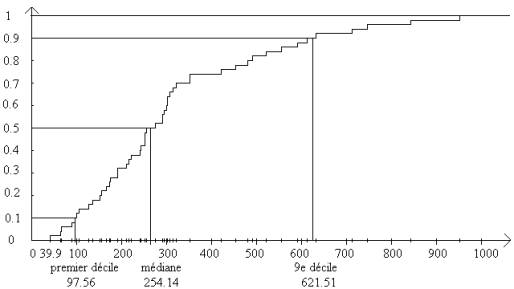
Figure 2.2 : Fonction de répartition des achats
On constate que la proportion d’achats
augmentent assez vite pour les petits montants, et plus lentement à partir
d’environ 215F.
4.2 Quantiles, quartiles, déciles ...
Plutôt que d’étudier la fonction de répartition elle– même, on préfère souvent en déduire les « quantiles » , qui caractérisent la répartition des n observations en classes de même effectif.
On n’utilise les quantiles que lorsque le nombre d’observations est suffisant. On peut considérer que les classes doivent avoir un effectif d’au moins 5 observations, d’où les conditions d’effectifs proposées ci-dessous :
|
mé |
deux classes d’effectifs n/2 |
(50%) |
n³10 |
|
|
les quartiles |
q1, q2 = mé, q3 |
quatre classes d’effectifs n/4 |
(25%) |
n³20 |
|
les quintiles |
r1, r2, r3, r4, r5 |
cinq classes d’effectifs n/5 |
(20%) |
n³25 |
|
Les déciles |
d1, d2, ..., d9 |
dix classes d’effectifs n/10 |
(10%) |
n³50 |
|
Les centiles |
c1, c2, ..., c99 |
cent classes d’effectifs n/100 |
(1%) |
n³500 |
Ces paramètres présentent les mêmes inconvénients de calcul que la médiane : il n’est pas toujours facile de les déterminer. Par exemple, les quartiles d’une série de 50 observations n’existent pas. On considère alors des approximations :
· Le premier quartile est défini par toute valeur comprise entre la 12e et de la 13e observation ;
· le deuxième quartile (la médiane) est défini par toute valeur comprise entre la 25e et de la 26e observation ;
· le troisième quartile est défini par toute valeur comprise entre la 47e et de la 48e observation .
En général (mais une interpolation linéaire est possible), on considère les moyennes des observations précédentes pour donner une valeur précise aux quartiles.
Les millimes, les dix-millimes, les cent-millimes, qui correspondent aux fractions 1/1000, 1/10 000, 1/100 000 de l’effectif total, sont utilisés par l’INSEE pour caractériser les séries d’observations très nombreuses.
Une première application des quantiles est la vérification de la symétrie de la répartition. Dans la pratique, on considérera que la répartition est symétrique si :
· La médiane et la moyenne sont à peu près égales ;
· La médiane est à peu près la moyenne des quartiles q1 et q3, des déciles d1 et d9, d2 et d8, etc…
Une seconde application des quantiles est le calcul du rapport entre la plus petite et la plus grande des valeurs d’une série d’observations. Dans la mesure où ces observations sont tirées au hasard, ce rapport peut varier considérablement d’un tirage à l’autre et son instabilité le rend discutable. On préfère calculer le rapport du dernier dix-millime ou cent-millime au premier. C’est ce que fait l’INSEE en étudiant les revenus ou les patrimoine des Français.
Exemple : Pour calculer les quantiles des achats des 50 clients, on classe les observations suivant les valeurs croissantes (tableau 6.1 du chapitre 1).
On définit les déciles comme les moyennes des observations de rang 5 et 6, de rangs 10 et 11, 15 et 16 etc.… Nous les avons représentés en figure 3. On obtient :
|
d1
= 97.560 |
d2
=152.405 |
d3
= 190.665 |
d4
= 241.340 |
d5
= 264.140 |
|
d6
= 300.575 |
d7
= 335.670 |
d8
= 484.715 |
d9
= 621.515 |
d10
= 951.160 |
Nous pouvons maintenant introduire une autre règle pour évaluer la taille d’une observation.
|
f.d.r. |
caractérisation |
Pourcentages |
|
F(x) < 0.025 |
x est très petite |
2.5% |
|
0.025< F(x) < 0.15 |
x est petite |
12.5% |
|
0.85< F(x) < F(0.975) |
x est grande |
12.5% |
|
F(x)>0.975 |
x est très grande. |
2.5% |
Tableau 3.2 : seconde règle de classification des valeurs
On ne compare pas ici une valeur x à la moyenne des observations : le raisonnement consiste à dire par exemple que quelqu’un, de taille x, est très grand parce que la plupart des gens sont plus petits que lui (F(x) >0.975) ou encore parce que peu de gens sont plus grands que lui.
L’avantage de cette règle par rapport à la première est de donner toujours des résultats cohérents avec les observations.
Exemple : on donne dans le tableau 6.1 du chapitre 1 la liste des achats classés par valeur croissante. Il est facile d’en déduire un classement des achats :
Achats d’un montant très faible (2.5% de 50, 1 valeur) : x5
Achats d’un montant faible (12.5% de 50, 6 valeurs) : x28, x4, x3, x29, x30, x31
Achats d’un montant élevé (12.5% de 50, 6 valeurs) : x9, x8, x12, x11, x39, x37
Achats d’un montant très élevé (2.5% de 50, 1 valeur) : x27
4.3 Concentration
Le coefficient de concentration de Gini. est un paramètre concernant des données positives ou nulles, dont l’interprétation est intéressante en économie et marketing, et qui caractérise « la courbe de concentration ».
Les observations sont classées suivant les valeurs croissantes : on les note comme précédemment x(i), i = 1, …n. L’observation x(1) est donc la plus petite valeur, x(n) la plus grande. Ces observations étant toutes positives, on a x(1) ³ 0.
Au nombre k on associe la somme des k plus petites valeurs x(i), i = 1, …, k..
|
|
|
|
k |
|
|
k |
––––––® |
S(k) = |
S |
x(i) |
|
|
|
|
i = 1 |
|
Au nombre n on associe donc la somme des n plus petites valeurs, ou la somme des n valeurs :
|
|
|
|
n |
|
|
n |
––––––® |
S(n) = |
S |
x(i) |
|
|
|
|
i = 1 |
|
A la proportion p = k/n, on associe la proportion de la somme des k plus petites valeurs, et l’on définit ainsi la courbe de concentration :
Définition : on appelle courbe de concentration la représentation graphique de la fonction définie par :
|
p = k/n |
–––––® |
C(p) =S(k)/S(n) |
Exemple numérique : calculons la courbe de concentration dans le cas des données suivantes : x1= 112, x2 = 151, x3 = 210, x4 = 225, x5 = 230, x6 = 354, x7=360, x8 = 450. On calcule la somme de toutes les valeurs :
|
|
8 |
|
|
|
S(8)
= |
S |
xi |
= 2092 |
|
|
i = 1 |
|
|
On a :
|
p = 1/8 |
C(p) = 112/2092 |
= 0.054 |
|
p = 2/8 |
C(p) = (112 + 151)/2092 |
= 0.126 |
|
p = 3/8 |
C(p) = (112 + 151 + 210)/2092 |
= 0.226 |
|
p = 4/8 |
C(p) = (112 + 151 + 210 + 225)/2092 |
= 0.334 |
|
p = 5/8 |
C(p) = (112 + 151 + 210 + 225 + 230)/2092 |
=
0.444 |
|
p
= 6/8 |
C(p)
= (112 + 151 + 210 + 225 + 230 + 354)/2092 |
=
0.613 |
|
p
= 7/8 |
C(p)
= (112 + 151 + 210 + 225 + 230 + 354 + 360)/2092 |
=
0.785 |
|
p
= 8/8 |
C(p)
= (112 + 151 + 210 + 225 + 230 + 354 + 360 + 450)/2092 |
=
1 |
D’où la courbe de concentration :
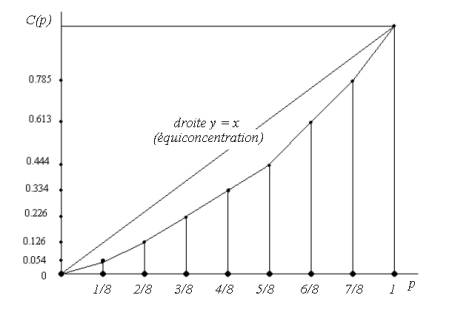
Figure 3.2 : courbe de concentration
(exemple précédent)
![]() On dit qu’il y a équiconcentration quand les
k plus petites valeurs, en proportion
On dit qu’il y a équiconcentration quand les
k plus petites valeurs, en proportion
p = k/n, représentent la même proportion p de la somme totale quel que soit k :
|
|
k |
S(k) |
|
p = |
––– |
= ––––– |
|
|
n |
S(n) |
Cette équiconcentration est caractérisée par la droite y = x représentée sur la figure 4.
Nous admettons ici les propriétés suivantes, certaines étant démontrées dans les compléments pédagogiques du cédérom.
· L’équiconcentration signifie que les observations sont constantes ;
· La fonction C(p) est croissante et égale à 1 pour p = 1 (ou k = n) ;
· C(p) est toujours inférieur à p, ce qui signifie que la courbe de concentration est toujours en dessous de la droite y = x.
· C(p) augmente de plus en plus vite.
Comme
on peut le constater sur la figure 4 ci-dessus, l’aire comprise entre la droite
y = x et la courbe de concentration varie de 0 à 0.5. L’usage en statistique
étant d’utiliser des paramètres variant de 0 à 1, on définit le coefficient de
Gini par le double de cette aire :
Définition : on appelle coefficient de concentration g de Gini le double de l’aire comprise entre la droite y = x et la courbe de concentration.
Son calcul n’est pas simple. On peut utiliser la formule suivante, dans laquelle m est la moyenne des xi (Saporta, p. 124):
|
|
|
n |
n |
|
|
|
|
S |
S |
çxi – xj ç |
|
|
|
i = 1 |
j = i +1 |
|
|
g |
= |
––––––––––––––––––––– |
||
|
|
|
n ( n – 1 ) m |
||
Les propriétés du coefficient de Gini sont les suivantes : :
· Plus le coefficient est proche de 1, plus la somme dépend des observations les plus grandes.
·
Plus le coefficient est proche de 0, moins la somme
dépend des observations les plus grandes.
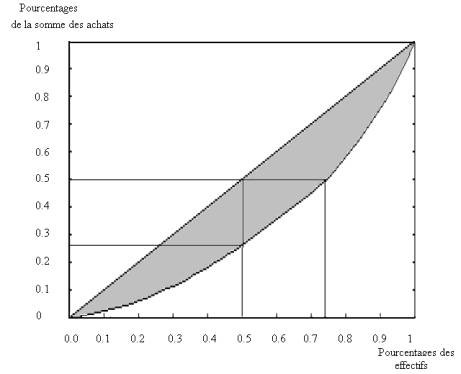
Exemple : La courbe de concentration des achats de la clientèle d’Euromarket est donnée en figure 4.
Les 50% plus petits achats représentent à peu près 27% du total des ventes. Il faut considérer les 75% (environ) plus petits achats pour obtenir la moitié du chiffre d’affaire. On peut dire aussi que les 25% clients les plus importants réalisent la moitié du chiffre d’affaires ou encore que le montant de leurs achats est le double de la moyenne.
L’aire
totale du carré est égale à 1, et le coefficient de concentration de Gini est
le double de l’aire colorée en gris. Il est ici égal à 0.35 : la
concentration des achats n’est pas très forte, et la perte de quelques gros
clients n’aurait pas d’effet important sur le chiffre d’affaires total.