On entend souvent qu’un schéma vaut mieux qu’un long discours. Effectivement, lorsque l’on veut étudier une série d’observations statistiques, il est souvent judicieux de commencer par en donner une représentation graphique.

Cette représentation dépend de la nature des données étudiées. En effet, il existe plusieurs types de données : données quantitatives continues (mesurées par une unité de grandeur, comme le mètre, le franc), quantitatives discrètes (résultant d’un dénombrement et s’exprimant en nombres entiers) ou qualitatives (codées par une lettre, par exemple F pour féminin, M pour masculin, ou un chiffre sans signification numérique) et ordinales (objets classés par ordre de préférence).

Les représentations graphiques fondamentales sont :

· des diagra m mes, dans le cas de données qualitatives, quantitatives discrètes ou ordinales ;

· des histogrammes, dans le cas de données quantitatives.

Exemple : Le directeur commercial de l’hypermarché EUROMARKET se propose de comparer la structure socioprofessionnelle et les achats de sa clientèle à ceux des autres hypermarchés de la chaîne. Sa démarche consiste à étudier la CSP de clients tirés au hasard à la sortie des caisses ainsi que leurs achats( tableau 2.1). On trouvera les données complètes en anne xe.

On note bien entendu F le sexe féminin et M le sexe masculin. La catégorie socioprofessionnelle (CSP) est définie par les 7 groupes de professions ci-dessous :

1. Agri : agriculteur ; ouvrier agricole	2. Ouv. : ouvrier
3. Emp. : employé ;	4. C.M. : cadre moyen ;
5. C.Sup. : cadre supérieur;	6. PIC : Commerçants, artisans ;
7. Inact. : inactifs, retraités, chômeurs, étudiants

Tableau 1.1 : Liste des catégories socioprofessionnelles

1	Agri.	M	150.15	26	PIC	F	314.25
2	Ouv.	F	173.12	27	Inact.	F	951.16
3	C.Sup	F	88.91	28	PIC	F	63.22
4	C.M.	M	65.10	29	C.M.	M	95.22
5	Inact.	F	39.90	30	Emp.	M	99.90
6	C.Sup.	F	351.15	31	PIC	M	104.57
7	Emp.	F	478.80	32	C.M.	M	452.75
8	Emp.	F	745.33	33	Emp.	F	190.68
9	Ouv.	M	841.50	34	Ouv.	F	220.36
10	C.M.	F	555.10	35	Emp.	M	250.66
11	Agri.	F	632.13	36	C.Sup.	M	250.87
12	Ouv.	F	712.22	37	Ouv.	F	590.14
13	Emp.	M	254.13	38	C.M.	F	301.25
14	Ouv.	F	301.52	39	Agri.	M	610.90
15	Emp.	M	420.15	40	Emp.	F	125.34
16	Emp.	F	289.90	41	Emp.	F	240.90
17	Ouv.	F	251.14	42	Emp.	F	290.75
18	Emp.	M	190.65	43	Emp.	M	241.78
19	C.M.	F	215.85	44	Emp.	F	305.90
20	Emp.	F	165.44	45	C.M.	F	520.45
21	Emp.	F	174.55	46	Ouv.	M	490.63
22	Emp.	F	135.33	47	Inact.	M	210.33
23	Ouv.	M	154.66	48	C.M.	M	350.44
24	PIC	F	274.15	49	Inact.	F	320.90
25	C.Sup.	M	293.12	50	Ouv.	M	299.90

Tableau 2.1 : Catégories socioprofessionnelles et achats

des 50 clients de EUROMARKET

1. Diagrammes.

Il est facile de représenter graphiquement la répartition des observations suivant une variable qualitative, ordinale ou quantitative codée par valeurs entières. Il existe de nombreuses méthodes, disponibles sur la plupart des tableurs comme Excel, et les erreurs sont dues fréquemment à des choix malheureux.

1.1 Généralités. Diagrammes de base.

Dans le cas général des données qualitatives, la variable qualitative est constituée de « modalités » dont le codage peut être effectué par des caractères alphabétiques (par exemple, F pour Féminin, M pour Masculin) mais il est fréquent, pour faciliter le traitement informatique des données, d’utiliser un codage numérique (1 pour Féminin, 2 pour Masculin).

La plupart des erreurs, dans les graphiques concernant les variables qualitatives, viennent de ce codage par des chiffres qui n’a en réalité aucun sens numérique ni ordinal. La CSP agriculteur, codée par 1, n’est pas « avant » la CSP ouvrier, codée par 2. Le sexe peut être codé par 1 pour Féminin et par 2 pour Masculin ou inversement, cela n’a aucune importance. L’ordre des valeurs n’a pas de sens particulier et peut être modifié.

Les variables quantitatives discrètes sont définies par des grandeurs numériques exprimées en nombres entiers. Le nombre d’enfants par foyer en est un exemple, de même que le nombre de personnes attendant l’autobus à un arrêt, faisant la queue à une caisse d’un hypermarché etc.…Ces variables sont quantitatives : on peut en calculer et en interpréter la m o y enne. On peut les représenter par des diagrammes comme les variables qualitatives, mais le codage a un sens numérique, et on ne peut inverser l’ordre des valeurs.

Il existe deux diagrammes de base : un diagra m me en bâtons, appelé fréquemment et improprement histogramme, et un diagr a mme circulaire.

Ces diagrammes représentent les effectifs ou les pourcentages de l’échantillon suivant chaque modalité de la variable qualitative :

· Le diagramme en bâtons est élémentaire : on reporte le long de l’axe des abscisses la liste des modalités de la variable et le long de l’axe des ordonnées l’effectif de l’échantillon correspondant à chacune d’entre elles.

· Le diagramme circulaire est constitué d’un disque représentant la totalité de l’échantillon. Chaque modalité de la variable qualitative est caractérisée par un secteur circulaire dont l’aire, et par suite l’angle au centre, représente l’effectif de l’échantillon correspondant.

Il est préférable dans la quasi totalité des cas de représenter non les effectifs correspondant à chaque modalité ou à chaque valeur entière, mais les proportions. Les deux méthodes sont équivalentes, mais la représentation des pourcentages permet de comparer deux diagrammes entre eux indépendamment des effectifs totaux.

On peut créer d’autres graphiques à partir de ces deux types de diagrammes, par juxtaposition, superposition etc. On peut aussi trier les modalités dans l’ordre des effectifs décroissants, l’objectif étant alors de classer les modalités.

Certains logiciels proposent des graphiques très élaborés, dont la compréhension devient cependant difficile ; le but de ces graphiques est plus commercial que de fournir un outil statistique de qualité.

1.2 Diagrammes d’EXCEL.

L’assistant du tableur EXCEL propose un certain nombre de graphiques, parmi lesquels des histogrammes (qui sont en réalité des diagrammes en bâtons) et des graphiques circulaires (figure 1.1) :

Parmi les histogrammes, on choisit un des formats suivants (figure 2.1):

La variété offerte dans le choix du diagramme a pour réciproque le danger de sélectionner un type de schéma ne convenant pas aux données étudiées. Ceux qui proposent une représentation de valeurs négatives (types 1, 2, 4, 6, 7 et 8) sont à éviter en statistique et conviennent pour représenter des résultats financiers par exemple.

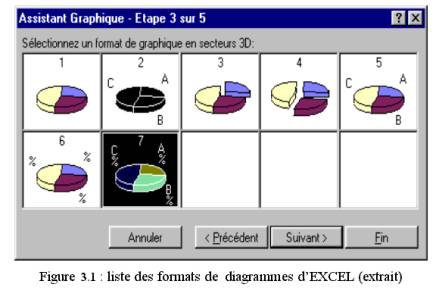
Les diagrammes circulaires peuvent être créés sous forme d’ellipses donnant une représentation dans l’espace (3D) pour améliorer l’esthétique( figure 3.1) :

1.3 Exemples.

Les répartitions des clients du tableau 2.1 sont les suivantes :

Sexe	Effectifs	Catégorie socioprofessionnelle	Effectifs
1. sexe féminin :	30	1. Agriculteur :	3
2. sexe masculin :	20	2. Ouvrier :	10
		3. Employé :	17
		4. Cadre moyen :	8
		5. Cadre supérieur :	4
		6. Commerçants, artisans :	4
		7. Inactifs :	4

Les diagrammes en bâtons donnés en figures 4.1, 5.1, 6.1, 7.1, 8.1 ont été obtenus par Excel :

On notera que dans les figures 4.1 à 7.1, ce sont les effectifs qui sont reportés en ordonnée. Il est préférable que ce soient les proportions, ou les pourcentages, par homogénéité avec la procédure générale et pour faciliter les comparaisons de diagrammes établis à partir d’ensembles de données différents.

Le diagramme donné en figure 5.1 représente les effectifs par catégorie socioprofessionnelle. Ces CSP ont été classées suivant les effectifs décroissants : les employés sont très nombreux parmi les clients, les ouvriers et les cadres moyens sont à peu près deux fois moins nombreux. Les autres CSP ne sont guère présentes dans l’échantillon.

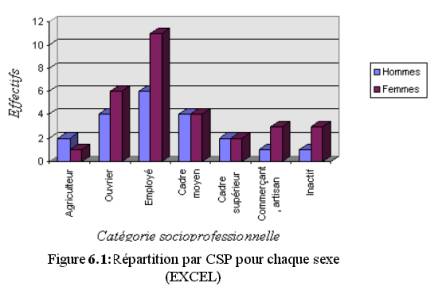
On peut calculer aussi les répartitions des hommes et des femmes suivant la CSP, et les représenter simultanément. On obtient un diagramme en bâtons permettant de comparer les effectifs et non les proportions : la différence est importante, puisqu’il y a 30 femmes et 20 hommes.

	Femmes :	Hommes
Agriculteur :	1	2
Ouvrier :	6	4
Employé :	11	6
Cadre moyen :	4	4
Cadre supérieur :	2	2
Commerçant, artisan :	3	1
Inactif :	3	1

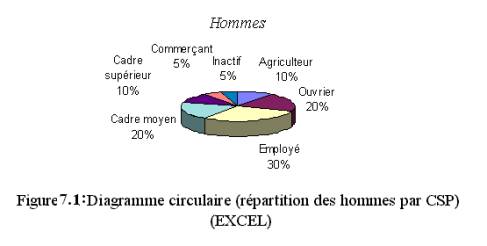
Le premier diagramme circulaire ci-dessous représente la répartition des hommes suivant la catégorie socioprofessionnelle et est obtenu avec un effet en trois dimensions :

Le second, qui représente la répartition des femmes suivant la catégorie socioprofessionnelle, se présente sous la forme d’un disque.

L’aire S d’un secteur circulaire caractérisant une proportion p de l’échantillon doit être égale à une proportion p de l’aire A du disque. En notant Q son angle au centre, on a les angles suivants dans le cas de la répartition des femmes :

p = 0.03	Q = 0.03 x 360	=	10.8°	p = 0.07	Q = 0.07 x 360	=	25.2°
p = 0.10	Q = 0.10 x 360	=	36°	p = 0.13	Q = 0.13 x 360	=	46.8°
p = 0.20	Q = 0.20 x 360	=	72°	p = 0.37	Q = 0.37 x 360	=	133.2°

Lorsque l’aire totale du disque caractérise le nombre total d’observations, l’aire de chaque secteur caractérise l’effectif de la modalité correspondante. En construisant deux disques, on peut alors comparer la répartition des hommes à celles des femmes suivant les CSP en pourcentages (caractérisés par les angles) et en effectifs (caractérisés par les aires).

2. Répartitions d’observations quantitatives.

Nous abordons ici le cas de variables quantitatives appelées continues, caractérisées par le fait qu’elles peuvent prendre n’importe quelle valeur entre deux valeurs données.

2.1 Choix des classes.

La procédure la plus simple consiste à répartir les observations dans des intervalles appelés aussi classes préalablement définis. Il n’existe pas de méthode générale pour définir ces classes ; les choix sont effectués par l’utilisateur qui doit évidemment tenir compte des données, de leur nature et des informations dont il dispose a priori.

En ce qui concerne le nombre de classes, on peut donner comme valeur approximative le nombre d’observations divisé par dix. Toutefois, il est souvent recommandé de considérer un nombre de classes impair, pour disposer d’une classe centrale souvent utile dans les représentations graphiques. Pour 60 observations, on choisira donc 5 ou 7 classes plutôt que 6. Cette règle ne s’applique évidemment qu’aux effectifs relativement faibles, et il est dans la plupart des cas inutile de considérer 100 classes si le nombre d’observations est égal à 1000.

Les bornes des classes ne sont pas faciles à choisir. Les choix dépendent toujours de l’utilisateur et des données, ils sont « empiriques », c’est-à-dire choisis de façon raisonnée.

Une première difficulté est de fixer la plus petite et la plus grande des bornes. La question posée est la suivante : entre quelles valeurs varient les données ? On peut choisir la valeur la plus petite et la valeur la plus grande des valeurs observées ; on peut aussi déterminer les valeurs les plus vraisemblables, mais ce n’est pas toujours facile.

En ce qui concerne les classes suivantes, plusieurs critères peuvent être utilisés :

· on fixe les bornes de façon arbitraire, en tenant compte de la nature des données, de la lisibilité des résultats numériques ;

· on fixe les bornes de façon que les classes soient de même longueur ; l’avantage est la simplicité du calcul et de la représentation graphique ;

· on fixe les bornes de façon que les classes soient de même effectif ; la démarche est plus riche d’informations mais elle demande plus de calculs et n’est pas toujours possible.

Dans chaque cas, la borne inférieure d’un intervalle est égale à la borne supérieure du précédent (sauf évidemment dans le cas de la première classe), de façon à recouvrir l’ensemble des valeurs possibles. Une façon d ‘éviter que des valeurs observées soient égales à une borne est de définir des bornes avec un nombre de décimales supérieur à celui des observations. Mais cela n’empêche pas les difficultés qui apparaissent lorsque des observations sont égales entre elles dans une proportion non négligeable par rapport à l’effectif de l’intervalle où elles sont classées.

On indique en général pour chaque classe son centre, le nombre d’observations qu’elle contient (appelé effectif absolu ou fréquence absolue) et le pourcentage d’observations dans la classe (appelé effectif relatif ou fréquence relative).

Dans le cas d’une répartition en intervalles de même longueur, les calculs ne posent pas de problèmes : on peut choisir un grand nombre de classes, effectuer la répartition des observations et réunir ensuite des classes entre elles. Nous proposons donc la règle suivante, qui peut aboutir à une répartition dans des intervalles de longueurs différentes :

· on choisit comme nombre de classes le nombre d’observations divisé par cinq ;

· on considère des classes de même longueur ;

· on effectue la répartition des observations ;

· on réunit les classes voisines dont les effectifs sont faibles, inférieurs à 5 par exemple, de façon à obtenir un nombre impair de classes et égal à peu près à l’effectif des observations divisé par dix. Les première et dernière classes peuvent contenir des effectifs plus faibles.

Exemple : Nous répartissons les achats des 50 clients en 10 classes de même longueur. Nous choisissons comme bornes extrêmes la plus petite et la plus grande des valeurs observées : 39.9 et 951.16. La longueur des classes est donnée par :

(951.16 - 39.9 )/10 = 91.126

Les bornes des autres classes sont les suivantes :

39.9 + 91.126 = 131.026	131.026 + 91.126 = 222.152
222.152 + 91.126 = 313.278	313.278+ 91.126 = 404.404
404.404+ 91.126 = 495.530	495.530+ 91.126 = 586.656
586.656+ 91.126 = 677.782	677.782+ 91.126 =768.908
768.908+ 91.126 =860.034	860.034+ 91.126 =951.160

On donne ci-dessous la répartition des 50 observations dans ces 10 classes :

Classe		Inf.	Sup.		centre	Eff.	%
1	[	39.900,	131.026	[	85.463	8	16
2	[	131.026,	222.152	[	176.589	11	22
3	[	222.152,	313.278	[	267.715	14	28
4	[	313.278,	404.404	[	358.841	4	8
5	[	404.404,	495.530	[	449.967	4	8
6	[	495.530,	586.656	[	541.093	2	4
7	[	586.656,	677.782	[	632.219	3	6
8	[	677.782,	768.908	[	723.345	2	4
9	[	768.908,	860.034	[	814.471	1	2
10	[	860.034,	951.160	]	905.597	1	2

Tableau 3.1 : répartition des achats en 10 classes de même longueur

Les classes données en tableau 3.1 sont trop nombreuses : les sept dernières regroupent chacune moins de cinq observations. Nous proposons de réunir les classes 4, 5 et 6 d’une part, les classes 7, 8, 9, 10 d’autre part. La répartition définitive est la suivante :

Classe		Inf.	Sup.		Centre	Eff.	%
1	[	39.900,	131.026	[	85.463	8	16
2	[	131.026,	222.152	[	176.589	11	22
3	[	222.152,	313.278	[	267.715	14	28
4	[	313.278,	586.656	[	449.967	10	20
5	[	586.656	951.160	]	768.908	7	14

Tableau 4.1 : répartition des achats en 5 classes après regroupement

On notera que les 5 classes précédentes ne sont pas de même longueur. Les bornes ne sont pas explicites et un lecteur ne comprendra pas la façon dont elles ont été choisies. On choisit donc des classes plus lisibles comme celles qui sont données dans le tableau 5.1.

2.2 Algorithmes.

Un algorithme est un procédé de calcul constitué d’une suite d’opérations. Il existe trois algorithmes classiques pour trier les observations :

· Le premier consiste à rechercher les observations de la classe 1, puis de la classe 2, de la classe 3 etc.… Il est nécessaire de parcourir la liste des observations autant de fois qu’il y a de classes.

· Le deuxième consiste à déterminer, pour chaque observation, la classe à laquelle elle appartient et à en déduire ensuite le nombre d’observations dans chaque classe. On ne parcourt la liste qu’une seule fois.

· On peut aussi classer les observations suivant les valeurs croissantes, et intercaler les bornes choisies. Il ne reste plus qu’à compter le nombre d’observations entre deux bornes.

Le second algorithme est plus rapide que le premier dans la plupart des cas et provoque moins d’erreurs. Le troisième demande plus de calculs mais donne une plus grande souplesse dans le choix des classes. Dans certains cas, il est utile de disposer de la liste des observations appartenant à chaque classe.

Exemple : dans les calculs ci-dessous, la borne inférieure de chaque intervalle est incluse, la borne supérieure exclue, sauf dans le dernier intervalle où elle est incluse.

· Répartition des achats des 50 clients en 5 classes définies empiriquement.

Le choix de bornes entières rend facile à lire la répartition obtenue :

Classes		Inf.	Sup.		centres	Eff.	%
1	[	0,	200	[	100	16	32
2	[	200,	300	[	250	14	28
3	[	300,	400	[	350	7	14
4	[	400,	600	[	500	7	14
5	[	600,	1000	]	800	6	12

Tableau 5.1 : répartition des achats en 5 classes arbitraires.

Pour répartir les observations dans ces cinq classes, on peut procéder de l’une des deux façons ci-dessous :

1. On compte les achats inférieurs à 200 F, puis les achats compris entre 200F et 300F, entre 300F et 400F, etc.…

2. On affecte chaque achat à la classe à laquelle il appartient : l’observation n°1 x₁=150.15 appartient à la classe 1, x₂, x₃, x₄, x₅ aussi, x₆ appartient à la classe 3, x₇ à la classe 4 etc.… Après avoir parcouru ainsi toute la liste des valeurs, on en déduit les effectifs par classe.

· Répartition des achats dans des classes de même effectif.

On commence par les ordonner suivant les valeurs croissantes (en ligne) :

n°	achats	n°	achats	n°	achats	n°	achats	n°	achats
5	39.90	28	63.22	4	65.10	3	88.91	29	95.22
30	99.90	31	104.57	40	125.34	22	135.33	1	150.15
23	154.66	20	165.44	2	173.12	21	174.55	18	190.65
33	190.68	47	210.33	19	215.85	34	220.36	41	240.90
43	241.78	35	250.66	36	250.87	17	251.14	13	254.13
24	274.15	16	289.90	42	290.75	25	293.12	50	299.90
38	301.25	14	301.52	44	305.90	26	314.25	49	320.90
48	350.44	6	351.15	15	420.15	32	452.75	7	478.80
46	490.63	45	520.45	10	555.10	37	590.14	39	610.90
11	632.13	12	712.22	8	745.33	9	841.50	27	951.16

Tableau 6.1 : achats des 50 clients ordonnés par valeurs croissantes

Dans le tableau 6.1, l’observation n°1 : 150.15, est placée en 10^ième position, l’observation n°2 en 13^ième position etc..

Chaque classe doit contenir le même nombre d’observations : pour 5 classes et 50 observations, l’effectif est donc égal à 10.

La première borne est égale à la plus petite valeur observée, 39.9. La suivante peut être tout nombre compris entre la 10^ième valeur et de la 11^ième valeur. On considère dans la plupart des cas leur moyenne : (150.15 + 154.66 )/2. De la même façon, on considère la moyenne de la 20^ième et de la 21^ième : ( 240.90 + 241.78 )/2 etc. La dernière borne est la plus grande valeur observée : 951.16. On obtient la répartition suivante :

Classes		Inf.	Sup.		centres	Eff.	%
1	[	39.9000,	152.4050	[	96.1525	10	20
2	[	152.4050,	241.3400	[	196.8725	10	20
3	[	241.3400,	300.5750	[	270.9575	10	20
4	[	300.5750,	484.7150	[	392.6450	10	20
5	[	484.7150,	951.1600	[	717.9375	10	20

Tableau 7.1 : répartition des achats en 5 classes de même effectif

La répartition des observations est intéressante en fait par les bornes qu’elle donne, qui sont des « quantiles ». Dans le cas ci-dessus, chaque classe regroupe 20% des observations : les bornes sont les quintiles. La notion de quantile est détaillée dans le chapitre 2.

3. Histogrammes.

Dans toutes les analyses statistiques, on donne une représentation graphique particulière de la rép a r t iti on des observations, appelée « h isto gra mme ». Il s’agit mathématiquement de la représentation approximative d’une fonction appelée d e n si té, dont l’interprétation est analogue à la densité classique utilisée par exemple en démographie, et dont nous introduisons la n otion théori que dans le chapitre 4.

Cette notion de densité dépend de l’unité de mesure utilisée pour effectuer les observations et les classer dans des intervalles.

3.1 Notion de densité.

En géographie on définit la densité de population par le nombre d’habitants par unité d’aire, en général par km² et on la calcule dans des zones géographiques parfaitement définies (par exemple, les villes, les états, …). C’est ainsi que l’on divise la population de la France (60 millions d’habitants) par sa superficie (550 000 km²) pour trouver le nombre d’habitants au km²(109 h/km²). On peut calculer la densité par région, par département, etc.

La densité statistique est analogue, mais pour obtenir des valeurs indépendantes du nombre total d’observations, on préfère utiliser les proportions d’observations plutôt que les effectifs. On la calcule ensuite dans chacun des intervalles préalablement définis pour répartir les observations, en divisant la proportion d’observations par la longueur de l’intervalle. Mathématiquement, c’est une approximation de la « densité de probabilité ». (cf. chapitre 4).

Définition : on appelle densité de la série (x_i) i = 1, …, n dans l’intervalle [a, b [ la proportion d’observations par unité de mesure dans cet intervalle.

Le calcul es t le suivant :

· soit p la proportion d’observations contenue dans la classe [a, b [.

· la densité est donnée par d = p/[b-a] dans tout l’intervalle [a, b [.

Exemple : on considère la répartition des achats des 50 clients suivant les intervalles arbitraires préalablement choisis (tableau 5.1). La densité est calculée de la façon suivante :

Classe 1 : d = 0.32/200 = 0.0016	Classe 2 : d = 0.28/100 = 0.0028
Classe 3 : d = 0.14/100 = 0.0014	Classe 4 : d = 0.14/200 = 0.0007
Classe 5 : d = 0.12/400 = 0.0003

On présente souvent les résultats sous la forme suivante :

Classe		Inf.	Sup.		longueur	%	densité
1	[	0,	200	[	200	32	0.0016
2	[	200,	300	[	100	28	0.0028
3	[	300,	400	[	100	14	0.0014
4	[	400,	600	[	200	14	0.0007
5	[	600,	1000	]	400	12	0.0003

Tableau 8.1 : densité dans le cas de 5 classes de longueurs différentes.

Dans le cas de 10 classes de même longueur, on obtient le tableau 9.1. La longueur des classes étant constante, la densité est directement proportionnelle à la fréquence relative ou encore au nombre des observations qui lui appartiennent. Cette particularité est à l’origine de l’erreur fréquente consistant à reporter en ordonnée les pourcentages au lieu de la densité dans le tracé de l’histogramme.

Classe		Inf.	Sup.		longueur	%	densité
1	[	39.9000,	131.0260	[	91.126	16	0.00176
2	[	131.0260,	222.1520	[	91.126	22	0.00241
3	[	222.1520,	313.2780	[	91.126	28	0.00307
4	[	313.2780,	404.4040	[	91.126	8	0.00088
5	[	404.4040,	495.5300	[	91.126	8	0.00088
6	[	495.5300,	586.6560	[	91.126	4	0.00044
7	[	586.6560,	677.7820	[	91.126	6	0.00066
8	[	677.7820,	768.9080	[	91.126	4	0.00044
9	[	768.9080,	860.0340	[	91.126	2	0.00022
10	[	860.0340,	951.1600	[	91.126	2	0.00022

Tableau 9.1 : densité dans le cas de 10 classes de même longueur.

3.2 Représentation graphique de la densité : histogrammes.

définition : on appelle histogramme[1] la représentation graphique de la densité.

Il est construit de la façon suivante :

· en abscisse, on reporte les valeurs observées et les classes que l’on a définies ;

· en ordonnée, on reporte la densité.

Les valeurs observées sont quantitatives : l’ordre des classes et leur longueur sont imposés sur l’axe des abscisses et une modification de cet ordre ou le non-respect de la longueur n’a aucun sens. L’origine représente toujours la valeur 0 en ordonnée. Par contre, elle peut être choisie différemment sur l’axe des abscisse.

La proportion observée d’unités statistiques dans une classe est donc caractérisée par l’aire du rectangle correspondant.

Il est possible d’obtenir par des logiciels classiques des histogrammes, mais on prendra garde qu’en général, ces logiciels supposent que les classes sont de même longueur, et reportent en ordonnée les proportions, au lieu des densités. Les résultats qu’ils donnent lorsque les intervalles choisis sont de longueur variable sont donc erronés. C’est le cas en particulier d’EXCEL.

Exemple : Les densités calculées précédemment dans les tableaux 7.1, 8.1 et 9.1 sont représentée par les histogrammes ci-dessous :

Figure 9.1 : histogramme des achats suivant la répartition 7.1

Figure 10.1 : histogramme des achats suivant la répartition 8.1

Figure 11.1 : histogramme des achats suivant la répartition 9.1

3.3 Stabilité de l’histogramme. Classe modale. Courbe en cloche.

Il est évident que le choix des classes est fondamental dans le calcul de la densité et que des difficultés pratiques peuvent apparaître suivant les données étudiées.

Tout d’abord, la densité dans la première classe est très dépendante de sa borne inférieure dont le choix est arbitraire. De même, la densité dans la dernière classe dépend de sa borne supérieure.

Exemple : considérons comme borne inférieure 39.9 F au lieu de 0 F et comme borne supérieure 951.16 F au lieu de 1000 F (tableau 8.1). Les densités dans les classes 1 et 5 deviennent :

Classe 1 : d = 0.32/(200 - 39.90)	=	0.32/160.10 = 0.00200	(au lieu de 0.0016)
Classe 5 : d = 0.12/(951.16 - 600)	=	0.12/351.16 = 0.00034	(au lieu de 0.0003)

La relative stabilité de la densité laisse penser que le choix des valeurs extrêmes est correct.

Ensuite, la définition précédente utilise des intervalles de la forme [a, b [ : une observation égale à la borne a est donc prise en compte, à l’inverse d’une observation égale à la borne b. Si l’on préfère les intervalles de la forme ]a, b], on obtiendra la difficulté inverse. L’effectif peut donc être différent bien que la longueur de la classe soit toujours égale à b-a. Ces difficultés sont souvent présentes dans le cas de données entières (variables discrètes) : on peut les éviter en donnant des valeurs décimales aux bornes des intervalles. Dans tous les cas, un histogramme très dépendant du choix des classes n’est pas satisfaisant, et on recherche systématiquement des intervalles donnant une bonne stabilité à l’histogramme.

Les histogrammes pré cédents font apparaître une classe dont la densité est plus grande que les autres.

Définition : on appelle classe modale une classe dont la densité est supérieure à celles de ses deux voisines.

Une classe modale peut être unique : la répartition (ou l’histogramme) est dite « unimodale ». Lorsqu’il y en a plusieurs, elle est qualifiée de « plurimodale » ; ce dernier cas peut se produire lorsque les observations proviennent de populations différentes.

Les histogrammes donnés en figure 9, figure 10 et figure 11 sont unimodaux.

Il est souvent utile de superposer à l’histogramme la représentation graphique d’une densité théorique, appelée loi normale, qui se présente sous la forme d’une cour be en cloche. Nous verrons en effet que cette densité sert de référence dans de nombreux cas, et que la proximité de l’histogramme avec cette courbe est nécessaire pour appliquer des méthodes statistiques telles que tests, prévision, etc. On se gardera bien toutefois de représenter cette courbe en cloche manuellement : cette représentation nécessite des calculs compliqués et un tracé manuel donne en général des résultats très médiocres.

Exemple : nous avons représenté sur la figure 12 ci-dessous l’histogramme de la répartition donnée dans le tableau 4.1 et superposé à cet histogramme la courbe e n cloche caractéristique de la densité théorique de la loi normale. La superposition montre bien que la distribution des achats ne suit pas la loi normale.

[1] Il existe d’autres méthodes pour représenter une densité (estimation de la densité), cf. Saporta (1989).