distributions d’échantillonnage

Les programmes Simulation de … figurant dans le dossier Programmes d’applications pédagogiques permettent de simuler la loi uniforme continue, la loi normale, la loi exponentielle et la loi continue proposée dans l’exercice 3 du chapitre 5. Chaque échantillon simulé donne une moyenne et une variance.

La multiplication des échantillons permet donc de disposer d’un échantillon de moyennes et de variances : l’histogramme donne alors une approximation de la loi théorique sous-jacente, qui est comme on le sait la loi normale pour la moyenne : c’est le théorème de la limite centrale, et, dans le cas d’échantillons suivant la loi normale, la loi du c² pour la variance.

Les programmes Moyenne et variance de la loi … permettent d’effectuer cette multiplication. Deux objectifs sont visés par ces programmes : la convergence de la loi de probabilité de la moyenne vers la loi normale (théorème de la limite centrale) et celle de la variance d’un échantillon d’une v.a. X vers la loi du c² si la variable X suit la loi normale. Ces deux distributions sont appelées distributions d’échantillonnage.

En exécutant ces programmes, on constate que, dès le nombre de termes dont la calcule la moyenne est suffisant, l’histogramme observé sur un échantillon de moyennes est proche de la courbe en cloche caractéristique de la loi normale quelle que soit la loi de probabilité choisie et que cette proximité est observée lorsque l’on répète les simulations.

Le nombre de termes dont on calcule la moyenne dépend de la nature de la loi de probabilité, surtout de la symétrie de cette loi.

On constate aussi que la variance ne suit la loi du c² que si les observations sur lesquelles elle est calculée constituent un échantillon de la loi normale.

Nous donnons ci-dessous l’exemple de la loi uniforme continue sur [0,1]. Nous avons simulé 1000 échantillons de taille 100 : on obtient donc 1000 moyennes et 1000 variances dont nous donnons un extrait ci-dessous :

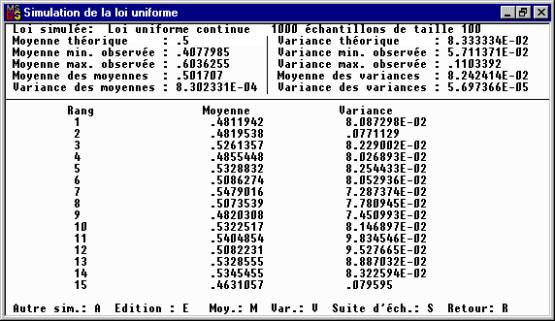
En appuyant sur M, on obtient l’histogramme des 1000 moyennes suivant le nombre de classes précédemment choisi (ici, 17) :

La proximité avec la loi normale est évidente. Il n’en est pas de même entre la loi du c² et l’histogramme des variances :

La conclusion est la suivante : lorsqu’une v.a. suit la loi uniforme, la v.a. M définie par la moyenne d’un échantillon de taille 100 suit la loi normale, mais la v.a. S² définie par la variance de l’échantillon ne suit pas la loi du c².

On pourra calculer pour un certain nombre d’échantillons les intervalles de confiance de la moyenne (pour des échantillons de taille suffisante de loi quelconque) et de la variance (pour des échantillons de la loi normale).