calcul de probabilités

On trouve, dans le dossier Tests et Tables statistiques de StatPC, le logiciel Tables statistiques concernant les lois continues et les lois discrètes.

On peut utiliser ces tables pour connaître la probabilité d’un événement donné, mais aussi pour illustrer quelques propriétés de ces lois de probabilités.

Considérons tout d’abord la table des lois de probabilité continues :

On choisit la loi normale de moyenne 10 d’écart type 2 ; en entrant comme valeur 9 et 11, on obtient la fenêtre ci-dessous :

On voit apparaître les propriétés suivantes :

· symétrie de la loi de probabilité par rapport à la moyenne ;

· somme des probabilités P( X <9) + P(9 < X < 11) + P( X > 11) égale à 1.

On pourra évidemment mettre cette symétrie en évidence sur la loi de Student, et étudier la convergence de la loi de Student vers la loi normale centrée réduite.

En ce qui concerne la loi de Fisher Snedecor, les deux fenêtres ci-dessous montrent la relation (évidente pour ceux qui connaissent la loi de Fisher Snedecor) entre F et 1/F :

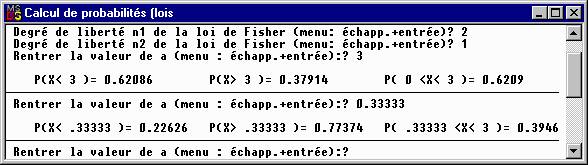
Les tables des lois de probabilités discrètes se présentent de la façon suivante (l binomiale de paramètres 10, 0.3):

En appuyant sur P et en donnant deux valeurs k₁ et k₂, on obtient comme on peut le voir sur la fenêtre précédente la probabilité P( k₁ £X £ k₂).

Cette facilité de calcul peut être utilisée pour montrer la convergence de la loi binomiale B(n,p) vers la loi de Poisson P(m) lorsque le produit n p tend vers m pour n suffisamment grand et p petit :

Par exemple, pour n p = 10 :

Pour la loi binomiale B(25,0.4) :	P( 10 £X £ 15) = 0.562214
Pour la loi binomiale B(50,0.2) :	P( 10 £X £ 15) = 0.525456
Pour la loi binomiale B(100,0.1) :	P( 10 £X £ 15) = 0.508819
Pour la loi de Poisson P(10) :	P( 10 £X £ 15) = 0. 493330

D’une façon plus générale, on peut concrétiser facilement les convergences de la loi binomiale et de la loi de Poisson vers la loi normale, ainsi que les relations entre les lois de probabilité que l’on trouvera dans l’ouvrage de Saporta (Probabilités, Analyse de données et Statistique, p.473).