Achats des clients d’Euromarket.
On considère les achats des 50 clients d’Euromarket (fichier de données Euromar.dat, de paramètres Euromar.par).
Tous les résultats peuvent être établis par StatPC.
1) Répartir les clients en 5 classes de même effectif. Construire l’histogramme de cette répartition. Commenter.
2) Calculer la moyenne, l’écart type et la médiane. Calculer le coefficient d’asymétrie. Ce coefficient peut-il être considéré comme proche de 0 ? Que peut-on en déduire à propos de la répartition des achats ?
3) Appliquer la règle de classification fondée sur la moyenne et l’écart type pour déterminer les achats particulièrement faibles ou élevés. L’utilisation de cette règle est-elle justifiée ? Sinon, appliquer une autre règle de classification pour déterminer les achats de montants faibles et élevés.
4) Comment s’appellent les bornes des cinq classes précédentes ? Construire la fonction de répartition approchée par ces bornes. Calculer les quartiles sur les données individuelles et par interpolation linéaire (on pourra se limiter à une approximation graphique).
5) Construire la courbe de concentration des achats. Quelle est la part du chiffre d’affaires réalisée par les 5 clients qui dépensent le moins ? Par les 5 clients qui dépensent le plus ? Comparer ces deux parts de chiffres d’affaires.
6) Donner une approximation graphique de la concentration aux quintiles. En déduire une valeur approximative du coefficient de concentration. Comparer à la valeur exacte donnée par logiciel.
Correction
1) On veut répartir les achats dans cinq classes de même effectif. Le logiciel donne les résultats suivants :
|
Classe |
Centre |
Effectif |
Pourcentages |
Densité |
|
[ 39.9000 , 152.4050 [ |
96.1525 |
10 |
20 |
0.0018 |
|
[ 152.4050 , 241.3400 [ |
196.8725 |
10 |
20 |
0.0022 |
|
[ 241.3400 , 300.5750 [ |
270.9575 |
10 |
20 |
0.0034 |
|
[ 300.5750 , 484.7150 [ |
392.6450 |
10 |
20 |
0.0011 |
|
[ 484.7150 , 951.1600 [ |
717.9375 |
10 |
20 |
0.0004 |

Les classes sont effectivement de même effectif égal à 10. Ce n’est pas toulours le cas, par exemple s’il existe des observations de même valeur. Elles ne sont pas de même longueur, et la classe dont la longueur est la plus petite est la classe modale puisque elle correspond à la densité maximale. C’est une propriété générale dans le cas de classes de même effectif. Sur cet exemple, c’est la classe 3.
2) Paramètres statistiques de la série des achats :
|
Moyenne |
Ecart-type |
Médiane |
|
316.945 |
207.1291 |
264.14 |
La médiane apparaît nettement inférieure à la moyenne : moins de la moitié des observations sont supérieures à la moyenne, et certaines sont donc très supérieures, comme le confirme le coefficient d’asymétrie :
|
Coefficient d’asymétrie : 1.16. |
Pour un effectif n = 50, les valeurs limites de la valeur absolue du coefficient d’asymétrie sont cas = 0.534 (5%) ou cas = 0.787 (1%). Le coefficient trouvé est trop grand (5%) et même beaucoup trop grand (1%) pour que la répartition puisse être considérée comme normale et symétrique.
Finalement, il est préférable de donner la médiane 264.14 pour caractériser l’ensemble des achats. En conclusion, les achats sont de l’ordre de 265F.
3) L’application de la règle de classification fondée sur la moyenne et l’écart type donne les résultats suivants :
Règle de classification :
|
m – 2 s |
m – s |
m |
m + s |
m + 2 s |
|
-97.31323 |
109.8159 |
316.945 |
524.0742 |
731.2033 |
|
Petits |
Effectif:
7 |
5 |
28 |
4 |
3 |
29 |
30 |
31 |
|
Grands |
Effectif:
5 |
10 |
37 |
39 |
11 |
12 |
|
|
|
Très
grands |
Effectif:
3 |
8 |
9 |
27 |
|
|
|
|
Il ne peut exister évidemment aucun achat inférieur à –97.31 (inférieurs à m – 2 s). Cette absence résulte de l’asymétrie de la répartition, déjà mise en évidence par le coefficient d’asymétrie. La règle utilisée précédemment ne convient donc pas pour classer de telles observations : il est préférable d’appliquer la seconde règle fondée sur la fonction de répartition :
|
achats |
pourcentage d’obs. inférieurs |
achats |
pourcentage d’obs. inférieurs |
|
39.90 |
2% |
555.10 |
86% |
|
63.22 |
4% |
590.14 |
88% |
|
65.10 |
6% |
610.90 |
90% |
|
88.91 |
8% |
632.13 |
92% |
|
95.22 |
10% |
712.22 |
94% |
|
99.90 |
12% |
745.33 |
96% |
|
104.57 |
14% |
841.50 |
98% |
Les pourcentages considérés étant pour simplifier 3% (valeurs très faibles), 13% (valeurs faibles) , 87% (valeurs élevées) et 97% (valeur très élevées), on peut considérer que les achats sont :
|
très faibles s’ils sont inférieurs à |
(39.9 + 63.22) / 2 |
= 51.56 F |
|
faibles s’ils sont inférieurs à |
(99.90 + 104.57)) / 2 |
= 102.235 F |
|
grands s’ils sont supérieurs à |
(555.10 + 590.14)) / 2 |
= 572.62 F |
|
très grands s’ils sont supérieurs à |
(745.33 + 841.50) / 2 |
= 795.415 F |
On dénombre donc un achat très faible (39.90F), cinq faibles (63.22, 65.10, 88.91, 95.22, 99.90), cinq élevés (590.14, 610.90, 632.13, 712.22, 745.33), et deux très élevés (841.50, 951.16). L’achat le plus petit, très inférieur au suivant, est ici considéré comme très faible. De même, l’achat de 745.33 est classé parmi les achats élevés et non très élevés : c’est plus cohérent puisqu’il est plus proche du précédent (712.22) que du suivant (841.50).
4) Les bornes des classes s’appellent les quintiles : ces classes regroupent en effet 20% de l’effectif total des observations.

Les quartiles rassemblent 25% de la population.
Le premier quartile q1 est à peu près au centre de l’intervalle [127, 224] : il est de l’ordre de 180.
Le second est par définition la médiane mé, entre 224 et 321, de l’ordre de 280.
Le troisième q3 est environ légèrement supérieur à 418. On choisit 430.
Nous avons calculé les quartiles par interpolation linéaire et sur les données individuelles. L’ensemble des résultats est donné ci-dessous :
|
|
Approximation graphique |
Interpolation linéaire |
Données individuelles |
|
q1
= |
180 |
174.64 |
169.28 |
|
mé
= |
280 |
270.96 |
264.14 |
|
q3
= |
430 |
438.68 |
385.65 |
L’approximation graphique donne des résultats très proches du calcul par interpolation linéaire, mais le troisième quartile est mal reconstruit par rapport à la valeur exacte.
5) Un nombre de cinq clients représente 10% de l’effectif total, soit une proportion de 10%. On en déduit graphiquement que les cinq plus petits achats (0.1 en abscisse) correspondent environ à 2% du montant total des achats (le chiffre d’affaires), tandis que les cinq plus grands correspondent à 25% (1 – 0.75) du chiffre d’affaires. Le rapport, égal à 12.5, donne un ordre de grandeur de la variation des achats : les achats varient approximativement dans un rapport de 1 à 12.5.
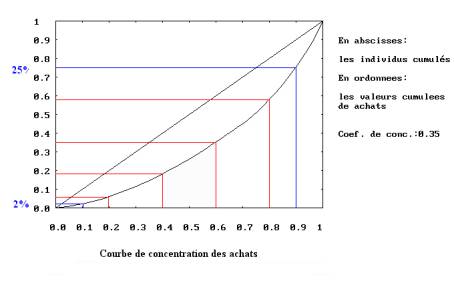
6) On considère la série des quintiles. Le calcul est facile :
Courbe de concentration de la variable X1
|
n° |
Proportion |
valeur |
part
de la somme totale |
concentration |
|
1 |
0.2 |
150.16 |
150.16 |
0.07080 |
|
2 |
0.4 |
240.9 |
391.06 |
0.18438 |
|
3 |
0.6 |
299.9 |
690.96 |
0.32578 |
|
4 |
0.8 |
478.8 |
1169.76 |
0.55153 |
|
5 |
1 |
951.16 |
2120.92 |
1.00000 |
Le calcul du coefficient de concentration par les quintiles consiste à déterminer l’aire représentée dans la figure ci-dessous et à la multiplier par deux. Cette aire est la somme des aires de deux triangles et de trois trapèzes, dont les bases sont représentées en bleu. On utilise les propriétés ci-dessous :
· L’aire d’un triangle est égale au produit de la hauteur et de la base divisée par deux.
· L’aire d’un trapèze est égale au produit de la hauteur et de la somme des bases divisée par deux.
· La diagonale du carré a pour équation y = x.
On remarque que dans le calcul, la hauteur est toujours la même (0.2 dans le cas des quintiles), et que chaque base, parallèle à l’axe des ordonnée, est égale à la précédente et de la forme p – c(p), où p est la proportion (0.2, 0.4, 0.6, 0.8, 1) et c(p) la concentration en p (0.07080 , 0.18438, 0.32578, 0.55153,1).

|
Longueur de la base du premier triangle : |
0.2 – 0.0708 = 0.1292 |
|
|
|
Aire du triangle 1 : |
0.1292 x 0.2 /2 |
= |
0.01292 |
|
|
|
|
|
|
Longueur de la première base du premier trapèze : |
0.2 – 0.0708 = 0.1292 |
|
|
|
Longueur de la seconde base du trapèze : |
0.4 – 0.1844 = 0.2156 |
|
|
|
Aire du trapèze 2: |
(0.1292 + 0.2156) x 0.2 /2 |
= |
0.03448 |
|
|
|
|
|
|
Longueur de la première base du deuxième trapèze :
|
0.4 – 0.18438 = 0.2156 |
|
|
|
Longueur de la seconde base du trapèze : |
0.6 – 0.32578 = 0.2742 |
|
|
|
Aire du trapèze 3 : |
(0.2156 + 0.2742) x 0.2 /2 |
= |
0.04898 |
|
|
|
|
|
|
Longueur de la première base du troisième trapèze
: |
0.6 – 0.32578 = 0. 2742 |
|
|
|
Longueur de la seconde base du trapèze : |
0.8 – 0.55153 = 0.24847 |
|
|
|
Aire du trapèze 4 : |
(0.2485 + 0.2742) x 0.2 /2 |
= |
0.05227 |
|
|
|
|
|
|
longueur de la base du dernier triangle : |
0.8 – 0.55153 = 0. 24847 |
|
|
|
Aire du triangle 5 : |
0.2485 x 0.2 /2 |
= |
0.02485 |
|
|
|
|
|
|
Somme des aires : |
|
= |
0.173 |
|
|
|
|
|
|
Coefficient de concentration : |
0.173 x 2 |
= |
0.346 |
|
coefficient de concentration |
|
|
valeur approchée : 0.346 |
valeur exacte : 0.35 |