L’analyse
de l’image et des graphiques
Thierry Foucart
L’analyse des graphiques (histogrammes, nuages de points, etc.) est une pratique courante en statistique. Elle s’incrit dans le contexte général de l’analyse de l’image.
Nous donnons ci-dessous un placard publicitaire commandé par Volkswagen et publié dans différents journaux au mois de mars 2001.
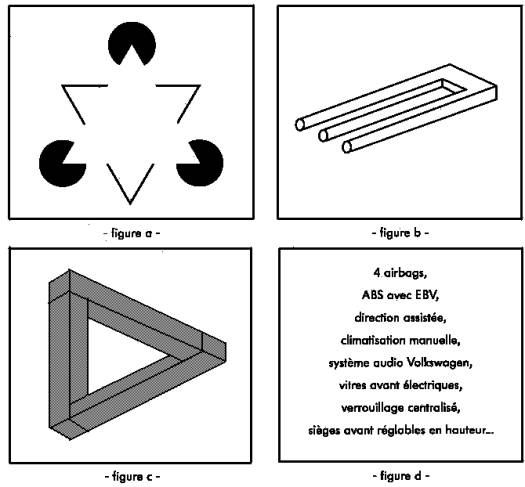
La figure a, en haut à gauche, montre un triangle blanc, dont les sommets sont les disques noirs, et qui n’existe pas. On notera la rémanence de ce triangle, que l’on continue de voir même après avoir effacé une partie du dessin. Le dessinateur voulait nous montrer un triangle, nous l’avons vu parce que nous avons l’habitude de voir un triangle placé de cette façon, et continuons de le voir. On aurait pu voir un triangle dont le milieu des côtés sont effacés, mais son orientation « la tête en bas » n’est pas habituelle. L’habitude nous guide dans l’interprétation de ce graphique.
La figure b, en haut à droite, représente un objet. On peut la couper en deux, dans le sens vertical : la partie gauche montre trois tuyaux, la partie droite un U couché. Nous avons du mal à comprendre ce qui ne va pas dans ce dessin lorsque nous l’examinons sans attention particulière. Lorsque le regard glisse de la gauche vers la droite, on s’aperçoit que les bords du tuyau central deviennent les bords des branches du U, et l’œil ne parvient pas à saisir l’objet dans sa globalité. En réalité, cet objet n’existe pas.
Dans la figure c, c’est l’espace qui est tordu : nous avons l’impression d’un triangle à trois angles droits, et là encore, il faut un effort d’attention pour comprendre comment ce dessin est construit et que l’objet qu’il représente est inconcevable.
La personne qui regarde ces schémas suit en fait une démarche personnelle. Ils sont examinés en fonction des critères propres à chacun, et sur la figure a où je vois un triangle blanc, un autre verra un triangle noir ou une étoile. Un enfant sera peut-être beaucoup moins gêné par la figure b, et ne verra pas l’impossibilité physique de la figure c. Cette démarche est influencée aussi par le discours qui est tenu : l’affirmation que la figure a représente un triangle ou une étoile a un effet évident sur la façon de regarder le schéma : le discours, le graphique et l’habitude personnelle se confortent les uns les autres.
Cette publicité veut de
toute évidence montrer qu’il faut se méfier des dessins, qu’il vaut mieux un
discours précis comme celui qui donne la liste des équipements proposés sur la
Volkswagen Polo Match (cadre d), et que la meilleure solution est d’aller voir
la voiture aux journées portes ouvertes des concessionnaires.
Les graphiques précédents ont donc pour rôle de renforcer le discours. L’argumentation est claire : les images peuvent mentir, et ne pas représenter la réalité : c’est en cela que cette publicité attire l’œil et qu’elle se veut efficace, en provoquant la confusion entre la réalité et le discours tenu en d.
Cette publicité consiste finalement à montrer des images fausses pour renforcer la crédibilité du discours. C’est une démarche originale fondée sur une contradiction : en règle générale en effet, l’image cherche à représenter la réalité et la démarche est fondée sur la confirmation du discours par l’image et inversement.
Encore faut-il savoir examiner, observer le dessin. Ce n’est pas toujours facile, en peinture en particulier, parce que les artistes peintres ont des objectifs plus difficiles à atteindre et utilisent des techniques beaucoup plus élaborées. C’est ainsi qu’un collectionneur a commandé à Paul Gauguin un tableau représentant un cheval blanc, et, considérant que le cheval représenté n’était pas blanc, a finalement refusé le tableau produit. On trouve une reproduction de ce tableau à l'adresse suivante : http://www.france5.fr/education/gauguin/09enseignants/page06.html
C’est en se demandant pourquoi l’artiste a peint le cheval en vert que
l’on comprend qu’il est blanc. La réussite de l’artiste est alors totale :
le spectateur comprend la démarche que le peintre a suivie pour atteindre son
objectif. Un cheval peint en blanc aurait paru complètement saugrenu dans le
tableau, alors qu’en lui donnant les couleurs qui l’environnent, en indiquant
des taches d’ombre, le peintre montre des reflets qui caractérisent la seule
robe possible du cheval : blanc. Cette démarche n’est pas immédiate :
beaucoup d’observateurs réagissent comme le commanditaire de ce tableau et ne
comprennent pas que le cheval est blanc.
C’est là une différence importante entre le dessin publicitaire, destiné à être compris par tout le monde, même (ou peut-être de préférence) inconsciemment, et le dessin artistique, qui demande un effort de compréhension à l’observateur.
Mais un mathématicien, un sociologue, un psychologue, plus généralement
un scientifique n’est dans l’exercice de son métier ni un publicitaire, ni un
artiste peintre, ni un poète. La science appelle un chat un chat, exige un
discours direct, et l’analyse d’une représentation graphique doit être
évidente, accompagnée d’un discours explicatif clair. L’observateur d’un schéma
a alors tendance à oublier l’idée a priori qui a guidé son auteur.
En statistique, la représentation graphique doit visualiser les
propriétés des données étudiées. La démarche exploratoire est ici montrée dans
sa difficulté : on veut construire un graphique montrant les propriétés
des données que l’on étudie, soit, mais lesquelles ? Comment montrer ce
que l’on ne connaît pas ? Il y a un paradoxe que nous retrouvons dans
l’analyse quantitative : la méthode adaptée pour détecter les propriétés
des données dépend elle-même de ces propriétés. Il est donc indispensable, pour
concevoir un schéma, d’avoir une certaine connaissance préalable des données,
issue de d’analyses antérieures. Le schéma a alors pour but de monter la
justesse de cette connaissance, des idées a priori de son auteur. Par
suite, la figure ne fait que confirmer ces idée a priori : elle ne
la prouve pas. D’ailleurs, la statistique ne donne jamais de preuve.
Le graphique ci-dessous donne
l’évolution du nombre de tués sur les routes françaises
et les mesures de sécurité routières prises au cours de la période étudiée
(revue Automoto, août 99) : limitation de la vitesse à 50 km/h en
agglomération, port de la ceinture de sécurité obligatoire à l’arrière,
introduction du permis à points etc.
Une
interprétation superficielle laisse croire que ce graphique prouve que le
nombre de tués a diminué grâce aux
mesures prises. Mais c’est faux : ce n’est pas une preuve. On aurait pu
tout aussi bien indiquer les résultats des élections australiennes à la place
des mesures de sécurité et (ou) le taux annuel d’inflation à la place du nombre
de tués. On constaterait alors la coïncidence – apparente, créée par le
graphique – des évolutions sans que l’on puisse expliquer l’une par l’autre.
Pour prouver la relation de causalité entre la diminution du nombre de morts et une mesure de prévention routière, il faudrait vérifier l’impact de cette dernière sur les accidents survenus auparavant : c'est en examinant les circonstances dans lesquelles ils se sont produits et leurs conséquences sur les conducteurs et les passagers des véhicules que l'on peut évaluer l'efficacité de la mesure prise.

On peut donner un autre exemple de ce type de raisonnement erroné : une société publie dans une revue financière un graphique montrant la hausse du cours d'un fonds financier international de 1935 à nos jours, en indiquant comme précédemment pour un certain nombre de dates des événements caractéristiques de la période : il s'agit ici d'événements politiques tels que les guerres de 39-45, de Corée, d'Indochine, d'Algérie, du Vietnam … allant à l'évidence à l'encontre du développement économique.
L'objectif
est visiblement de montrer que la gestion du fonds a permis une croissance
quasi ininterrompue de la valeur financière de la part malgré tous ces événements. Pas plus que le précédent le
graphique n’est une preuve de cette affirmation : la démarche correcte
pour montrer la qualité des choix d’investissements est ici aussi de montrer
qu’ils ont été effectués de façon judicieuse à la suite de chacun de ces
événements.
L’exploitation
à des fins publicitaires de ce dernier graphique, pourtant construit comme le
premier, consiste finalement à inverser le raisonnement par rapport au
précédent, l’expression grâce à étant
changée par malgré.
Ces
exemples montrent que les démarches suivies pour analyser un graphique peuvent
être contradictoires et qu’elles ne sont pas uniquement rationnelles :
l’intuition, les idées a priori de l’examinateur jouent un rôle
important dans l’analyse du graphique construit à partir des idées a priori du
dessinateur. Dans la publicité de Volkswagen, l’impossibilité physique des
objets représentés a pour effet recherché d’augmenter la crédibilité du
discours. La confirmation du discours par le graphique est directe dans le
second graphique (grâce à) et inverse dans le troisième (malgré).
Finalement,
les graphiques sont présentés pour convaincre et non pour démontrer, le
contexte dans lequel ils sont présentés exercent une influence sur leur
interprétation, et il faut mener une réflexion critique sur la façon dont ils
sont construits avant d’admettre les propriétés qu’ils prétendent abusivement
prouver.